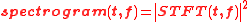Time-frequency analysis for music signal
Encyclopedia
Time–frequency analysis for music signals is one of the applications of time–frequency analysis. Musical sound can be more complicated than human vocal sound, occupying a wider band of frequency. Music signals are time-varying signals; while the classic Fourier transform is not sufficient to analyze them, time–frequency analysis is an efficient tool for such use. Time–frequency analysis is extended from the classic Fourier approach. Short-time Fourier transform
(STFT), Gabor transform
(GT) and Wigner distribution function
(WDF) are famous time–frequency methods, useful for analyzing music signals such as notes played on a piano, a flute or a guitar.
, and the sound of a violin is produced by bowing
. All musical sounds have their fundamental frequency
and overtones. Fundamental frequency is the lowest frequency in harmonic series. In a periodic signal, the fundamental frequency is the inverse of the period length. Overtones are integer multiples of the fundamental frequency.
In musical theory, pitch represents the perceived fundamental frequency of a sound. However the actual fundamental frequency may differ from the perceived fundamental frequency because of overtones.
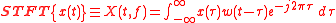
where w(t) is a window function
. When the w(t) is a rectangular function, the transform is called Rec-STFT. When the w(t) is a Gaussian function, the transform is called Gabor transform
.
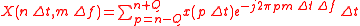
Let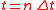
, 
, 
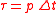and 
. There are some constraints of discrete short-time Fourier transform:
of the audio file shows in Figure 1. Spectrogram is the square of STFT, time-varying spectral representation. The spectrogram of a signal s(t) can be estimated by computing the squared magnitude
of the STFT of the signal s(t), as shown below:
Although the spectrogram is profoundly useful, it still has one drawback. It displays frequencies on a uniform scale. However, musical scales are based on a logarithmic scale for frequencies. Therefore, we should describe the frequency in logarithmic scale related to human hearing.
can also be used to analyze music signal. The advantage of Wigner distribution function is the high clarity. However, it needs high calculation and has cross-term problem, so it's more suitable to analyze signal without more than one frequency at the same time.
is:
where x(t) is the signal, and x*(t) is the conjugate of the signal.
Short-time Fourier transform
The short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
(STFT), Gabor transform
Gabor transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time...
(GT) and Wigner distribution function
Wigner distribution function
The Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....
(WDF) are famous time–frequency methods, useful for analyzing music signals such as notes played on a piano, a flute or a guitar.
Knowledge about music signal
Music is a type of sound that has some stable frequencies in a time period. Music can be produced by several methods. For example, the sound of a piano is produced by striking stringsStrings (music)
A string is the vibrating element that produces sound in string instruments, such as the guitar, harp, piano, and members of the violin family. Strings are lengths of a flexible material kept under tension so that they may vibrate freely, but controllably. Strings may be "plain"...
, and the sound of a violin is produced by bowing
Bow (music)
In music, a bow is moved across some part of a musical instrument, causing vibration which the instrument emits as sound. The vast majority of bows are used with string instruments, although some bows are used with musical saws and other bowed idiophones....
. All musical sounds have their fundamental frequency
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
and overtones. Fundamental frequency is the lowest frequency in harmonic series. In a periodic signal, the fundamental frequency is the inverse of the period length. Overtones are integer multiples of the fundamental frequency.
| Frequency | Order | ||
|---|---|---|---|
| f = 440 Hz | N = 1 | Fundamental frequency | 1st harmonic |
| f = 880 Hz | N = 2 | 1st overtone | 2nd harmonic |
| f = 1320 Hz | N = 3 | 2nd overtone | 3rd harmonic |
| f = 1760 Hz | N = 4 | 3rd overtone | 4th harmonic |
In musical theory, pitch represents the perceived fundamental frequency of a sound. However the actual fundamental frequency may differ from the perceived fundamental frequency because of overtones.
Short-time Fourier transform
Continuous STFT
Short-time Fourier transform is a basic type of time–frequency analysis. If there is a continue signal x(t), we can compute the short-time Fourier transform by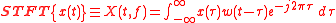where w(t) is a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
. When the w(t) is a rectangular function, the transform is called Rec-STFT. When the w(t) is a Gaussian function, the transform is called Gabor transform
Gabor transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time...
.
Discrete STFT
However, normally the musical signal we have is not a continuous signal. It is sampled in a sampling frequency. Therefore, we can’t use the formula to compute the Rec-short-time Fourier transform. We change the original form to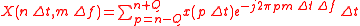Let
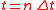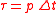, , and . There are some constraints of discrete short-time Fourier transform:
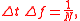where N is an integer.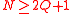
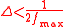, where 
is the highest frequency in the signal.
STFT example
Fig.1 shows the waveform of a piano music audio file with 44100 Hz sampling frequency. And Fig.2 shows the result of short-time Fourior transform (we use Gabor transform here) of the audio file. We can see from the time–frequency plot, from t = 0 to 0.5 second, there is a chord with three notes, and the chord changed at t = 0.5, and then changed again at t = 1. The fundamental frequency of each note in each chord is show in the time–frequency plot.Spectrogram
Figure 3 shows the spectrogramSpectrogram
A spectrogram is a time-varying spectral representation that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also...
of the audio file shows in Figure 1. Spectrogram is the square of STFT, time-varying spectral representation. The spectrogram of a signal s(t) can be estimated by computing the squared magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the STFT of the signal s(t), as shown below:
Although the spectrogram is profoundly useful, it still has one drawback. It displays frequencies on a uniform scale. However, musical scales are based on a logarithmic scale for frequencies. Therefore, we should describe the frequency in logarithmic scale related to human hearing.
Wigner distribution function
The Wigner distribution functionWigner distribution function
The Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....
can also be used to analyze music signal. The advantage of Wigner distribution function is the high clarity. However, it needs high calculation and has cross-term problem, so it's more suitable to analyze signal without more than one frequency at the same time.
Formula
The Wigner distribution function is:where x(t) is the signal, and x*(t) is the conjugate of the signal.
Sources
- Joan Serra, Emilia Gomez, Perfecto Herrera, and Xavier SerraXavier SerraXavier Serra is a researcher in the field of Sound and Music Computing and professor at the Pompeu Fabra University in Barcelona. He is the founder and director of the Music Technology Group at the UPF.-Life and Education:...
, "Chroma Binary Similarity and Local Alignment Applied to Cover Song Identification," August, 2008 - William J. Pielemeier, Gregory H. Wakefield, and Mary H. Simoni, "Time-frequency Analysis of Musical Signals," September,1996
- Jeremy F. Alm and James S. Walker, "Time-Frequency Analysis of Musical Instruments," 2002
- Monika Dorfler, "What Time-Frequency Analysis Can Do To Music Signals," April,2004
- EnShuo Tsau, Namgook Cho and C.-C. Jay Kuo, "Fundamental Frequency Estimation For Music Signals with Modified Hilbert–Huang transform" IEEE International Conference on Multimedia and Expo, 2009.