Tomographic reconstruction
Encyclopedia
The mathematical basis for tomographic imaging was laid down by Johann Radon
. It is applied in computed tomography
to obtain cross-sectional images of patients. This article applies in general to tomographic reconstruction for all kinds of tomography
, but some of the terms and physical descriptions refer directly to X-ray computed tomography.
The projection of an object at a given angle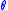
is made up of a set of line integrals. In X-ray CT, the line integral represents the total attenuation
of the beam of x-rays as it
travels in a straight line through the object. As mentioned above, the resulting image is a 2D (or 3D) model of the attenuation coefficient
. That is, we wish to find the image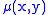
. The simplest and easiest way to visualise method of scanning is the system of parallel projection, as used in the first scanners. For this discussion we consider the data to be collected as a series of parallel rays, at position 
, across a projection at angle 
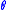. This is repeated for various angles. Attenuation occurs exponentially in tissue:
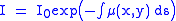
where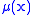
is the attenuation coefficient at position 
along the ray path. Therefore generally the total attenuation 
of a ray at position 
, on the projection at angle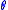 
, is given by the line integral:
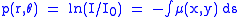
Using the coordinate system of Figure 1, the value of
onto which the point 
will be projected at angle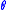 
is given by:
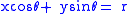
So the equation above can be rewritten as
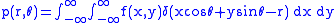
where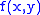
represents 
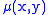. This function is known as the Radon transform
(or sinogram) of the 2D object. The projection-slice theorem
tells us that if we had an infinite number of one-dimensional projections of an object taken at an infinite number of angles, we could perfectly reconstruct the original object,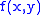
. So to get 
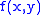back, from the above equation means finding the inverse Radon transform. It is possible to find an explicit formula for the inverse Radon transform. However, the inverse Radon transform proves to be extremely unstable with respect to noisy data. In practice, a stabilized and discretized version of the inverse Radon transform is used, known as the filtered back projection algorithm.
Johann Radon
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
. It is applied in computed tomography
Computed tomography
X-ray computed tomography or Computer tomography , is a medical imaging method employing tomography created by computer processing...
to obtain cross-sectional images of patients. This article applies in general to tomographic reconstruction for all kinds of tomography
Tomography
Tomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
, but some of the terms and physical descriptions refer directly to X-ray computed tomography.
The projection of an object at a given angle
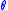is made up of a set of line integrals. In X-ray CT, the line integral represents the total attenuationAttenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
of the beam of x-rays as it
travels in a straight line through the object. As mentioned above, the resulting image is a 2D (or 3D) model of the attenuation coefficient
Attenuation coefficient
The attenuation coefficient is a quantity that characterizes how easily a material or medium can be penetrated by a beam of light, sound, particles, or other energy or matter. A large attenuation coefficient means that the beam is quickly "attenuated" as it passes through the medium, and a small...
. That is, we wish to find the image
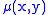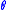. The simplest and easiest way to visualise method of scanning is the system of parallel projection, as used in the first scanners. For this discussion we consider the data to be collected as a series of parallel rays, at position , across a projection at angle . This is repeated for various angles. Attenuation occurs exponentially in tissue: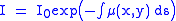where
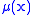is the attenuation coefficient at position along the ray path. Therefore generally the total attenuation of a ray at position , on the projection at angle 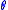, is given by the line integral: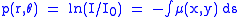Using the coordinate system of Figure 1, the value of
onto which the point will be projected at angle 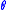is given by: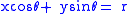So the equation above can be rewritten as
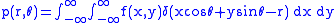
where
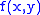represents 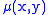. This function is known as the Radon transformRadon transform
thumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
(or sinogram) of the 2D object. The projection-slice theorem
Projection-slice theorem
In mathematics, the projection-slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:...
tells us that if we had an infinite number of one-dimensional projections of an object taken at an infinite number of angles, we could perfectly reconstruct the original object,
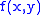. So to get 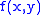back, from the above equation means finding the inverse Radon transform. It is possible to find an explicit formula for the inverse Radon transform. However, the inverse Radon transform proves to be extremely unstable with respect to noisy data. In practice, a stabilized and discretized version of the inverse Radon transform is used, known as the filtered back projection algorithm.Further reading
- Gabor HermanGabor HermanGabor T. Herman is a pioneer in the field of computed tomography, an important medical diagnostic procedure. He is also author of books on digital geometry and digital topology, 3D rendering in medicine and discrete tomography. He has written well over 100 research articles, including several...
(2009), Fundamentals of Computerized Tomography: Image Reconstruction from Projections, 2nd Edition, Springer, ISBN 978-1-85233-617-2. - Avinash KakAvinash KakAvinash C. Kak is a professor of Electrical and Computer Engineering at Purdue University who has done pioneering research in several different aspects of information processing...
& Malcolm Slaney (1988), Principles of Computerized Tomographic Imaging, IEEE Press, ISBN 0-87942-198-3.
External links
- http://www.slaney.org/pct/
- http://www.bronnikov-algorithms.com/Products.htm Software for tomographic reconstruction
- http://www.itk.org/ Insight ToolKit; open source tomographic support software