Tonality diamond
Encyclopedia
In music theory
and tuning
, a tonality diamond is a two-dimensional diagram of ratio
s in which one dimension is the Otonality and one the Utonality. Thus the n-limit
tonality diamond is an arrangement in diamond-shape of the set of rational number
s r,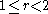
, such that the odd part of both the numerator and the denominator of r, when reduced to lowest terms, is less than or equal to the fixed odd number n. Equivalently, the diamond may be considered as a set of pitch class
es, where a pitch class is an equivalence class of pitches under octave
equivalence. The tonality diamond is often regarded as comprising the set of consonances
of the n-limit. Although originally invented by Max Meyer
, the tonality diamond is now most associated with Harry Partch
.
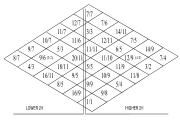
, and subdivided into (n+1)2/4 smaller rhombuses. Along the upper left side of the rhombus are placed the odd numbers from 1 to n, each reduced to the octave (divided by the minimum power of 2 such that
). These intervals are then arranged in ascending order. Along the lower left side are placed the corresponding reciprocals, 1 to 1/n, also reduced to the octave (here, multiplied by the minimum power of 2 such that 
). These are placed in descending order. At all other locations are placed the product of the diagonally upper- and lower-left intervals, reduced to the octave. This gives all the elements of the tonality diamond, with some repetition. Diagonals sloping in one direction form Otonalities
and the diagonals in the other direction form Utonalities. One of Partch's instruments, the diamond marimba, is arranged according to the tonality diamond.
7/4 5/3
13/8 14/9 3/2
3/2 13/9 7/5 15/11
11/8 4/3 13/10 14/11 5/4
5/4 11/9 6/5 13/11 7/6 15/13
9/8 10/9 11/10 12/11 13/12 14/13 15/14
1/1 1/1 1/1 1/1 1/1 1/1 1/1 1/1
16/9 9/5 20/11 11/6 24/13 13/7 28/15
8/5 18/11 5/3 22/13 12/7 26/15
16/11 3/2 20/13 11/7 8/5
4/3 18/13 10/7 22/15
16/13 9/7 4/3
8/7 6/5
16/15
, meaning all non-unison elements of the diamond are only one unit from the unison. The five-limit diamond then becomes a regular hexagon surrounding the unison, and the seven-limit diamond a cuboctahedron
surrounding the unison.
, which gives the number of positive integers less than n and relatively prime
to n, that is, it counts the integers less than n which share no common factor with n, and if d(n) denotes the size of the n-limit tonality diamond, we have the formula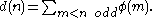
From this we can conclude that the rate of growth of the tonality diamond is asymptotically equal to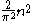
. The first few values are the important ones, and the fact that the size of the diamond grows as the square
of the size of the odd limit tells us that it becomes large fairly quickly. There are seven members to the 5-limit diamond, 13 to the 7-limit diamond, 19 to the 9-limit diamond, 29 to the 11-limit diamond, 41 to the 13-limit diamond, and 49 to the 15-limit diamond; these suffice for most purposes.
rewrites Partch's diamond to clarify its theoretical relationship to string lengths (as Partch used in his Kitharas) and his Moodswinger
instrument. Landman flips the ratios (5/4 becomes 4/5) and takes the complement
string part (1/5 instead of 4/5) to make them easier to understand.
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
and tuning
Musical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
, a tonality diamond is a two-dimensional diagram of ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s in which one dimension is the Otonality and one the Utonality. Thus the n-limit
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
tonality diamond is an arrangement in diamond-shape of the set of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s r,
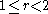, such that the odd part of both the numerator and the denominator of r, when reduced to lowest terms, is less than or equal to the fixed odd number n. Equivalently, the diamond may be considered as a set of pitch classPitch class
In music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
es, where a pitch class is an equivalence class of pitches under octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
equivalence. The tonality diamond is often regarded as comprising the set of consonances
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
of the n-limit. Although originally invented by Max Meyer
Max Meyer
Max Friedrich Meyer was a Professor of Experimental Psychology at the University of Missouri. He is co-developer of the Lipps–Meyer law. He was dismissed from the University of Missouri due to his academic involvement with a scandalous questionnaire issued by a student, Orval Hobart Mowrer...
, the tonality diamond is now most associated with Harry Partch
Harry Partch
Harry Partch was an American composer and instrument creator. He was one of the first twentieth-century composers to work extensively and systematically with microtonal scales, writing much of his music for custom-made instruments that he built himself, tuned in 11-limit just intonation.-Early...
.
The diamond arrangement
Partch arranged the elements of the tonality diamond in the shape of a rhombusRhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
, and subdivided into (n+1)2/4 smaller rhombuses. Along the upper left side of the rhombus are placed the odd numbers from 1 to n, each reduced to the octave (divided by the minimum power of 2 such that
). These intervals are then arranged in ascending order. Along the lower left side are placed the corresponding reciprocals, 1 to 1/n, also reduced to the octave (here, multiplied by the minimum power of 2 such that ). These are placed in descending order. At all other locations are placed the product of the diagonally upper- and lower-left intervals, reduced to the octave. This gives all the elements of the tonality diamond, with some repetition. Diagonals sloping in one direction form OtonalitiesOtonality and Utonality
Otonality and Utonality are terms introduced by Harry Partch to describe chords whose notes are the overtones or "undertones" of a given fixed tone. For example: 1/1, 2/1, 3/1,.....
and the diagonals in the other direction form Utonalities. One of Partch's instruments, the diamond marimba, is arranged according to the tonality diamond.
7-limit tonality diamond
| 7/4 Harmonic seventh The harmonic seventh interval , also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio . This is somewhat narrower than and is "sweeter in quality" than an "ordinary" minor seventh, which has a just-intonation ratio of 9:5 , or an equal-temperament ratio of... |
||||||
| 3/2 Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
7/5 Septimal tritone The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7... |
|||||
| 5/4 Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
6/5 | 7/6 Septimal minor third In music, the septimal minor third , also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5... |
||||
| 1/1 Unison In music, the word unison can be applied in more than one way. In general terms, it may refer to two notes sounding the same pitch, often but not always at the same time; or to the same musical voice being sounded by several voices or instruments together, either at the same pitch or at a distance... |
1/1 | 1/1 | 1/1 | |||
| 8/5 | 5/3 Major sixth In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two... |
12/7 | ||||
| 4/3 Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
10/7 Septimal tritone The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7... |
|||||
| 8/7 |
15-limit tonality diamond
15/87/4 5/3
13/8 14/9 3/2
3/2 13/9 7/5 15/11
11/8 4/3 13/10 14/11 5/4
5/4 11/9 6/5 13/11 7/6 15/13
9/8 10/9 11/10 12/11 13/12 14/13 15/14
1/1 1/1 1/1 1/1 1/1 1/1 1/1 1/1
16/9 9/5 20/11 11/6 24/13 13/7 28/15
8/5 18/11 5/3 22/13 12/7 26/15
16/11 3/2 20/13 11/7 8/5
4/3 18/13 10/7 22/15
16/13 9/7 4/3
8/7 6/5
16/15
Geometry of the tonality diamond
The five- and seven-limit tonality diamonds exhibit a highly regular geometry within the modulatory spaceModulatory space
The spaces described in this article are pitch class spaces which model the relationships between pitch classes in some musical system. These models are often graphs, groups or lattices...
, meaning all non-unison elements of the diamond are only one unit from the unison. The five-limit diamond then becomes a regular hexagon surrounding the unison, and the seven-limit diamond a cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
surrounding the unison.
Properties of the tonality diamond
Three properties of the tonality diamond and the ratios contained:- All ratios between neighboring ratios are superparticular ratios, those with a difference of 1 between numerator and denominatorFractionIn common usage a fraction is any part of a unit.Fraction may also mean:*Fraction , one of more equal parts of something, eg...
. For example: 2:1, 5:4, 9:8. - Ratios with relatively lower numbers have more space between them than ratios with higher numbers. For example: 2:1 (1200 cents), 3:2 (701.95 cents), 50:49 (34.98 cents), 49:48 (35.70 cents).
- The system, including the ratios between ratios, is symmetrical within the octave when measured in cents not in ratios.
Size of the tonality diamond
If φ(n) is Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
, which gives the number of positive integers less than n and relatively prime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n, that is, it counts the integers less than n which share no common factor with n, and if d(n) denotes the size of the n-limit tonality diamond, we have the formula
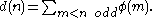
From this we can conclude that the rate of growth of the tonality diamond is asymptotically equal to
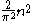. The first few values are the important ones, and the fact that the size of the diamond grows as the squareQuadratic growth
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity...
of the size of the odd limit tells us that it becomes large fairly quickly. There are seven members to the 5-limit diamond, 13 to the 7-limit diamond, 19 to the 9-limit diamond, 29 to the 11-limit diamond, 41 to the 13-limit diamond, and 49 to the 15-limit diamond; these suffice for most purposes.
Translation to string length ratios
Yuri LandmanYuri Landman
Yuri Landman is a Dutch experimental luthier who has made several experimental electric string instruments for a list of artists including Lee Ranaldo of Sonic Youth, Liars, Jad Fair of Half Japanese and Liam Finn...
rewrites Partch's diamond to clarify its theoretical relationship to string lengths (as Partch used in his Kitharas) and his Moodswinger
Moodswinger
The Moodswinger is a twelve string electric zither with an additional third bridge designed by Yuri Landman. The rod which functions as the third bridge divides the strings into two sections to cause an overtone multiphonic sound...
instrument. Landman flips the ratios (5/4 becomes 4/5) and takes the complement
Complement
In many different fields, the complement of X is something that together with X makes a complete whole—something that supplies what X lacks.Complement may refer to:...
string part (1/5 instead of 4/5) to make them easier to understand.