Topological conjugation
Encyclopedia
In mathematics
, two functions are said to be topologically conjugate to one another if there exists a homeomorphism
that will conjugate the one into the other. Topological conjugacy is important in the study of iterated function
s and more generally dynamical systems, since, if the dynamics of one iterated function can be solved, then those for any topologically conjugate function follow trivially.
To illustrate this directly: suppose that f and g are iterated functions, and there exists an h such that
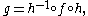
so that f and g are topologically conjugate. Then of course one must have
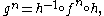
and so the iterated systems are conjugate as well. Here,
denotes function composition
.
and 
be topological space
s, and let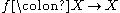
and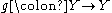 
be continuous function
s. We say that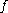
is topologically semiconjugate to 
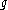, if there exists a continuous surjection 
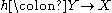such that 
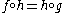. If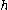 
is a homeomorphism
, then we say that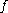
and 
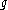are topologically conjugate, and we call 
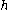a topological conjugation between 
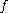and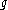 
.
Similarly, a flow
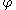on 
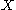is topologically semiconjugate to a flow 
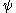on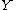 
if there is a continuous surjection 
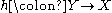such that 
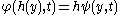for each 
, 
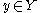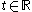. If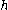 
is a homeomorphism then 
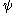and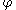 
are topologically conjugate.
in the space of all continuous surjections of a topological space to itself, by declaring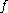
and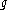 
to be related if they are topologically conjugate. This equivalence relation is very useful in the theory of dynamical system
s, since each class contains all functions which share the same dynamics from the topological viewpoint. For example, orbits
of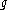
are mapped to homeomorphic orbits of 
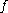through the conjugation. Writing 
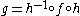makes this fact evident: 
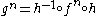. Speaking informally, topological conjugation is a “change of coordinates” in the topological sense.
However, the analogous definition for flows is somewhat restrictive. In fact, we are requiring the maps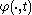
and 
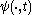to be topologically conjugate for each 
, which is requiring more than simply that orbits of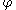 
be mapped to orbits of 
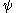homeomorphically. This motivates the definition of topological equivalence, which also partitions the set of all flows in 
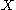into classes of flows sharing the same dynamics, again from the topological viewpoint.
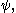and 
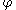are topologically equivalent, if there is a homeomorphism 
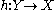, mapping orbits of 
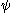to orbits of 
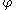homeomorphically, and preserving orientation of the orbits. In other words, letting 
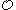denote an orbit, one has
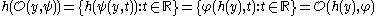
for each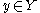
. In addition, one must line up the flow of time: for each 
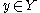, there exists a 
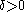such that, if 
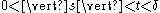, and if 
is such that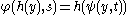 
, then 
.
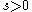Overall, topological equivalence is a weaker equivalence criterion than topological conjugacy, as it does not require that the time term is mapped along with the orbits and their orientation. An example of a topologically equivalent but not topologically conjugate system would be the non-hyperbolic class of two dimensional systems of differential equations that have closed orbits. While the orbits can be transformed each other to overlap in the spatial sense, the periods of such systems cannot be analogously matched, thus failing to satisfy the topological conjugacy criterion while satisfying the topological equivalence criterion.
1. Analogous systems defined as isomorphic dynamical systems
2. Adjoint dynamical systems defined via adjoint functors and natural equivalences in categorical dynamics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, two functions are said to be topologically conjugate to one another if there exists a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
that will conjugate the one into the other. Topological conjugacy is important in the study of iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
s and more generally dynamical systems, since, if the dynamics of one iterated function can be solved, then those for any topologically conjugate function follow trivially.
To illustrate this directly: suppose that f and g are iterated functions, and there exists an h such that
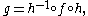
so that f and g are topologically conjugate. Then of course one must have
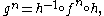
and so the iterated systems are conjugate as well. Here,
denotes function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
.
Definition
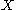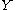Let and be topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, and let
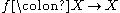and 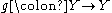be continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. We say that
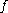is topologically semiconjugate to 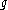, if there exists a continuous surjection 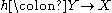such that 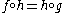. If 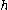is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, then we say that
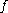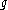and are topologically conjugate, and we call 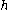a topological conjugation between 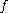and 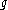.Similarly, a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
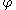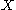on is topologically semiconjugate to a flow 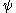on 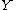if there is a continuous surjection 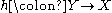such that 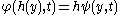for each 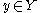, 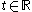. If 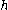is a homeomorphism then 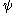and 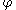are topologically conjugate.Examples
- the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
and the tent map are topologically conjugate. - the logistic map of unit height and the Bernoulli map are topologically conjugate.
Discussion
Topological conjugation defines an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
in the space of all continuous surjections of a topological space to itself, by declaring
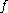and 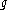to be related if they are topologically conjugate. This equivalence relation is very useful in the theory of dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, since each class contains all functions which share the same dynamics from the topological viewpoint. For example, orbits
Periodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
of
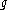are mapped to homeomorphic orbits of 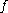through the conjugation. Writing 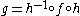makes this fact evident: 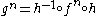. Speaking informally, topological conjugation is a “change of coordinates” in the topological sense.However, the analogous definition for flows is somewhat restrictive. In fact, we are requiring the maps
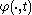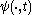and to be topologically conjugate for each , which is requiring more than simply that orbits of 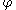be mapped to orbits of 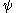homeomorphically. This motivates the definition of topological equivalence, which also partitions the set of all flows in 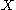into classes of flows sharing the same dynamics, again from the topological viewpoint.Topological equivalence
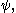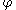We say that and are topologically equivalent, if there is a homeomorphism 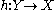, mapping orbits of 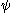to orbits of 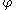homeomorphically, and preserving orientation of the orbits. In other words, letting 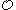denote an orbit, one has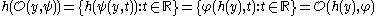for each
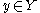. In addition, one must line up the flow of time: for each 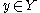, there exists a 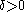such that, if 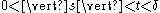, and if is such that 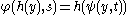, then 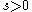.Overall, topological equivalence is a weaker equivalence criterion than topological conjugacy, as it does not require that the time term is mapped along with the orbits and their orientation. An example of a topologically equivalent but not topologically conjugate system would be the non-hyperbolic class of two dimensional systems of differential equations that have closed orbits. While the orbits can be transformed each other to overlap in the spatial sense, the periods of such systems cannot be analogously matched, thus failing to satisfy the topological conjugacy criterion while satisfying the topological equivalence criterion.
Generalizations of dynamic topological conjugacy
There are two reported extensions of the concept of dynamic topological conjugacy:1. Analogous systems defined as isomorphic dynamical systems
2. Adjoint dynamical systems defined via adjoint functors and natural equivalences in categorical dynamics.