
Toponogov's theorem
Encyclopedia
In the mathematical
field of Riemannian geometry
, Toponogov's theorem is a triangle comparison theorem. It is one of a family of theorems that quantify the assertion that a pair of geodesics emanating from a point p spread apart more slowly in a region of high curvature than they would in a region of low curvature.
Let M be an m-dimensional Riemannian manifold
with sectional curvature
K satisfying

Let pqr be a geodesic triangle in M, such that the geodesic pq is minimal and if δ ≥ 0, the length of the side pr is less than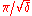 .
.
Let p′q′r′ be a geodesic triangle in the space form
Mδ such that the length of sides p′q′ and p′r′is equal to that of pq and pr respectively and the angle at p′ is equal to that at p.
Then
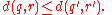
When the sectional curvature is bounded from above, a corollary to the Rauch comparison theorem
yields an analogous statement, but with the reverse inequality.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, Toponogov's theorem is a triangle comparison theorem. It is one of a family of theorems that quantify the assertion that a pair of geodesics emanating from a point p spread apart more slowly in a region of high curvature than they would in a region of low curvature.
Let M be an m-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
K satisfying

Let pqr be a geodesic triangle in M, such that the geodesic pq is minimal and if δ ≥ 0, the length of the side pr is less than
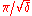 .
.Let p′q′r′ be a geodesic triangle in the space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
Mδ such that the length of sides p′q′ and p′r′is equal to that of pq and pr respectively and the angle at p′ is equal to that at p.
Then
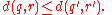
When the sectional curvature is bounded from above, a corollary to the Rauch comparison theorem
Rauch comparison theorem
In Riemannian geometry, the Rauch comparison theorem is a fundamental result which relates the sectional curvature of a Riemannian manifold to the rate at which geodesics spread apart. Intuitively, it states that for large curvature, geodesics tend to converge, while for small curvature,...
yields an analogous statement, but with the reverse inequality.

