
Torsionless module
Encyclopedia
In abstract algebra
, a module
M over a ring
R is called torsionless if it can be embedded into some direct product
RI. Equivalently, M is torsionless if each non-zero element of M has non-zero image under some R-linear functional f:

This notion was introduced by Hyman Bass
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is called torsionless if it can be embedded into some direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
RI. Equivalently, M is torsionless if each non-zero element of M has non-zero image under some R-linear functional f:

This notion was introduced by Hyman Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
.
Properties and examples
A module is torsionless if and only if the canonical map into its double dual,-
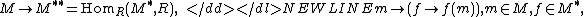
is injective. If this map is bijective then the module is called reflexive. For this reason, torsionless modules are also known as semi-reflexive.
- A free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
is torsionless. More generally, a direct sumDirect sumIn mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of torsionless modules is torsionless. - A submodule of a torsionless module is torsionless. In particular, any projective moduleProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
over R is torsionless; any left ideal of R is a torsionless left module, and similarly for the right ideals. - Let R be a domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
. Then any torsionless module is torsion-freeTorsion-freeIn mathematics, the term torsion-free may refer to several unrelated notions:* In abstract algebra, a group is torsion-free if the only element of finite order is the identity....
. - If R is a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
which is an integral domain and M is a finitely generated torsion-free module then M can be embedded into Rn and hence M is torsionless. - Since the rational numbers Q is a divisible abelian group, any Z-linear functional from Q to Z is zero. Thus Q is a torsion-free Z-module which is not torsionless.
- Suppose that N is a right R-module, then its dual N* has a structure of a left R-module. It turns out that any left R-module arising in this way is torsionless (similarly, any right R-module that is a dual of a left R-module is torsionless).
Relation with semihereditary rings
Stephen Chase proved the following characterization of semihereditary rings.
For any ring R, the following conditions are equivalent:- R is left semihereditary.
- All torsionless right R-modules are flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
. - The ring R is left coherentCoherent ringIn mathematics, a coherent ring is a ring in which every finitely generated left ideal is finitely presented.Many theorems about finitely generated modules over Noetherian rings can be extended to finitely presented modules over coherent rings....
and satsfies any of the four conditions that are known to be equivalent:- All right ideals of R are flat.
- All left ideals of R are flat.
- Submodules of all right flat R-modules are flat.
- Submodules of all left flat R-modules are flat.
- A free module

