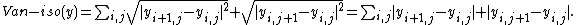Total variation denoising
Encyclopedia
In signal processing, Total variation denoising, also known as total variation regularization is a process, most often used in digital image processing
that has applications in noise removal. It is based on the principle that signals with excessive and possibly spurious detail have high total variation
, that is, the integral of the absolute gradient of the signal is high. According to this principle, reducing the total variation of the signal subject to it being a close match to the original signal, removes unwanted detail whilst preserving important details such as edges. The concept was pioneered by Rudin et al. in 1992.
This noise removal technique has advantages over simple techniques such as linear smoothing
or median filtering
which reduce noise but at the same time smooth away edges to a greater or lesser degree. By contrast, total variation denoising is remarkably effective at simultaneously preserving edges whilst smoothing away noise in flat regions, even at low signal-to-noise ratios .
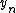, we can, for example, define the total variation as:
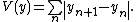
Given an input signal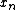
, the goal of total variation denoising is to find an approximation, call it 
, that has smaller total variation than 
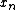but is "close" to 
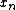. One measure of closeness is the sum of square errors:
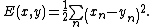
So the total variation denoising problem amounts to minimizing the following discrete functional over the signal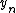
:
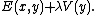
By differentiating this functional with respect to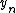
, we can derive a corresponding Euler-Lagrange equation
, that can be numerically integrated with the original signal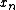
as initial condition. This was the original approach . Alternatively, since this is a convex functional
, techniques from convex optimization can be used to minimize it and find the solution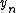
.
plays a critical role in the denoising process. When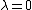 
, there is no denoising and the result is the same as the input signal. As 
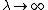, however, the total variation term plays an increasingly strong role, which forces the result to have smaller total variation, at the expense of being less like the input (noisy) signal. Thus, the choice of regularization parameter is critical to achieving just the right amount of noise removal.
The total variation norm proposed by the 1992 paper is
and is isotropic and not differentiable. A variation that is sometimes used, since it may sometimes be easier
to minimize, is an an-isotropic version
The standard total variation denoising problem is still of the form
where E is the 2D l2 norm. In contrast to the 1D case, solving this denoising is non-trivial. A recent algorithm that solves this is known as Chambolle's Algorithm.
Due in part to much research in compressed sensing
in the mid-2000s, there are many algorithms, such as the split-Bregman method, that solve variants of this problem.
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
that has applications in noise removal. It is based on the principle that signals with excessive and possibly spurious detail have high total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
, that is, the integral of the absolute gradient of the signal is high. According to this principle, reducing the total variation of the signal subject to it being a close match to the original signal, removes unwanted detail whilst preserving important details such as edges. The concept was pioneered by Rudin et al. in 1992.
This noise removal technique has advantages over simple techniques such as linear smoothing
Gaussian blur
A Gaussian blur is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail...
or median filtering
Median filter
In signal processing, it is often desirable to be able to perform some kind of noise reduction on an image or signal. The median filter is a nonlinear digital filtering technique, often used to remove noise. Such noise reduction is a typical pre-processing step to improve the results of later...
which reduce noise but at the same time smooth away edges to a greater or lesser degree. By contrast, total variation denoising is remarkably effective at simultaneously preserving edges whilst smoothing away noise in flat regions, even at low signal-to-noise ratios .
Mathematical exposition for 1D digital signals
For a digital signalDigital signal
A digital signal is a physical signal that is a representation of a sequence of discrete values , for example of an arbitrary bit stream, or of a digitized analog signal...
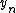, we can, for example, define the total variation as: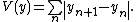Given an input signal
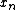, the goal of total variation denoising is to find an approximation, call it , that has smaller total variation than 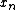but is "close" to 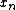. One measure of closeness is the sum of square errors: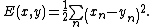So the total variation denoising problem amounts to minimizing the following discrete functional over the signal
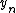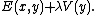
:By differentiating this functional with respect to
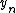, we can derive a corresponding Euler-Lagrange equationEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
, that can be numerically integrated with the original signal
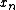as initial condition. This was the original approach . Alternatively, since this is a convex functionalConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, techniques from convex optimization can be used to minimize it and find the solution
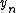.Regularization properties
The regularization parameter plays a critical role in the denoising process. When 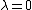, there is no denoising and the result is the same as the input signal. As 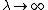, however, the total variation term plays an increasingly strong role, which forces the result to have smaller total variation, at the expense of being less like the input (noisy) signal. Thus, the choice of regularization parameter is critical to achieving just the right amount of noise removal.2D digital signals
We now consider 2D signals y, such as images.The total variation norm proposed by the 1992 paper is
and is isotropic and not differentiable. A variation that is sometimes used, since it may sometimes be easier
to minimize, is an an-isotropic version
The standard total variation denoising problem is still of the form
where E is the 2D l2 norm. In contrast to the 1D case, solving this denoising is non-trivial. A recent algorithm that solves this is known as Chambolle's Algorithm.
Due in part to much research in compressed sensing
Compressed sensing
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
in the mid-2000s, there are many algorithms, such as the split-Bregman method, that solve variants of this problem.
See also
- Total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
- Anisotropic diffusionAnisotropic diffusionIn image processing and computer vision, anisotropic diffusion, also called Perona–Malik diffusion, is a technique aiming at reducing image noise without removing significant parts of the image content, typically edges, lines or other details that are important for the interpretation of the image...
- Signal ProcessingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
- Digital Image ProcessingDigital image processingDigital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
- Noise reductionNoise reductionNoise reduction is the process of removing noise from a signal.All recording devices, both analogue or digital, have traits which make them susceptible to noise...