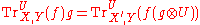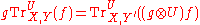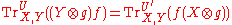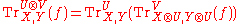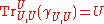Traced monoidal category
Encyclopedia
In category theory
, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.
A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions
called a trace, satisfying the following conditions:
(where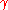 is the symmetry of the monoidal category).
is the symmetry of the monoidal category).
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.
A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions

called a trace, satisfying the following conditions:
- naturality in X: for every
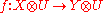 and
and 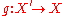 ,
,
- naturality in Y: for every
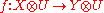 and
and  ,
,
- dinaturality in U: for every
 and
and 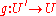
- vanishing I: for every
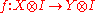 ,
,
- vanishing II: for every
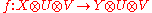
- superposing: for every
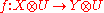 and
and 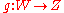 ,
,
- yanking:
(where
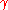 is the symmetry of the monoidal category).
is the symmetry of the monoidal category).Properties
- Every compact closed categoryCompact closed categoryIn category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
admits a trace.
- Given a traced monoidal category C, the Int construction generates the free (in some bicategorical sense) compact closure Int(C) of C.