
Trailing zero
Encyclopedia
In mathematics
, trailing zeros are a sequence of 0
s in the decimal
representation (or more generally, in any positional representation
) of a number, after which no other digit
s follow.
Trailing zeros to the right of a decimal point, as in 12.3400, do not affect the value of a number and may be omitted if all that is of interest is its numerical value. This is true even if the zeros recur infinitely. However, trailing zeros may be useful for indicating the number of significant figures, for example in a measurement. In such a context, "simplifying" a number by removing trailing zeros would be incorrect.
The number of trailing zeros in a base-b integer
n equals the exponent of the highest power of b that divides n. For example, 14000 has three trailing zeros and is therefore divisible by 1000 = 103. This property is useful when looking for small factors in integer factorization
. Binary numbers with many trailing zero bits are handled similarly in computer arithmetic.
of a non-negative integer
n, is simply the multiplicity of the prime
factor 5 in n! . This can be determined with this special case of de Polignac's formula
:
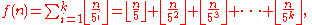
where k must be chosen such that

and ⌊a⌋ denotes the floor function
applied to a. For n = 0, 1, 2, ... this is
For example, 53 > 32, and therefore 32! = 263130836933693530167218012160000000 ends in

zeros. If n < 5, the inequality is satisfied by k = 0; in that case the sum is empty
, giving the answer 0.
The formula actually counts the number of factors 5 in n! , but since there are at least as many factors 2, this is equivalent to the number of factors 10, each of which gives one more trailing zero.
Defining
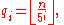
the following recurrence relation
holds:

This can be used to simplify the computation of the terms of the summation, which can be stopped as soon as q i reaches zero. The condition is equivalent to
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, trailing zeros are a sequence of 0
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
s in the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
representation (or more generally, in any positional representation
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
) of a number, after which no other digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s follow.
Trailing zeros to the right of a decimal point, as in 12.3400, do not affect the value of a number and may be omitted if all that is of interest is its numerical value. This is true even if the zeros recur infinitely. However, trailing zeros may be useful for indicating the number of significant figures, for example in a measurement. In such a context, "simplifying" a number by removing trailing zeros would be incorrect.
The number of trailing zeros in a base-b integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n equals the exponent of the highest power of b that divides n. For example, 14000 has three trailing zeros and is therefore divisible by 1000 = 103. This property is useful when looking for small factors in integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
. Binary numbers with many trailing zero bits are handled similarly in computer arithmetic.
Factorial
The number of trailing zeros in the decimal representation of n!, the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of a non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, is simply the multiplicity of the prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
factor 5 in n
De Polignac's formula
In number theory, de Polignac's formula, named after Alphonse de Polignac, gives the prime decomposition of the factorial n!, where n ≥ 1 is an integer. L. E. Dickson attributes the formula to Legendre.-The formula:...
:
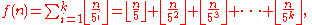
where k must be chosen such that

and ⌊a⌋ denotes the floor function
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
applied to a. For n = 0, 1, 2, ... this is
- 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 6, ... .
For example, 53 > 32, and therefore 32! = 263130836933693530167218012160000000 ends in

zeros. If n < 5, the inequality is satisfied by k = 0; in that case the sum is empty
Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
, giving the answer 0.
The formula actually counts the number of factors 5 in n
Defining
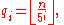
the following recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
holds:

This can be used to simplify the computation of the terms of the summation, which can be stopped as soon as q i reaches zero. The condition is equivalent to
External links
- Why are trailing fractional zeros important? for some examples of when trailing zeros are significant

