
Transition path sampling
Encyclopedia
Transition path sampling (TPS) is a method used in computer simulations of rare events, physical or chemical transitions of a system from one stable state to another that occur too rarely to be observed on a computer timescale. Examples include protein folding
, chemical reaction
s and nucleation
. Standard simulation tools such as molecular dynamics
can generate the dynamical trajectories of all the atoms in the system. However, because of the time gap between simulations and reality, even present supercomputers would require years of simulations to show an event that occurs once a μs.
Consider in general a system with two stable states A and B. The system will spend a long time in those states and occasionally jump from one to the other. There are many ways in which the transition can take place. Once a probability is assigned to each of the many pathways, one can construct a Monte Carlo
random walk in the path space of the transition trajectories, and thus generate the ensemble of all transition paths. All the relevant information can then be extracted from the ensemble, such as the reaction mechanism, the transition states, and the rate constants.
Given an initial path, TPS provides some algorithms to perturb that path and create a new one. As in all Monte Carlo walks, the new path will then be accepted or rejected in order to have the correct path probability. The procedure is iterated and the ensemble is gradually sampled.
A powerful and efficient algorithm is the so-called shooting move. Consider the case of a classical many-body system described by coordinates r and momenta p. Molecular dynamics generates a path as a set of (rt, pt) at discrete times t in [0,T] where T is the length of the path. For a transition from A to B, (r0, p0) is in A, and (rT, pT) is in B. One of the path times is chosen at random, the momenta p are modified slightly into p + δp, where δp is a random perturbation consistent with system constraints, e.g. conservation of energy and linear and angular momentum. A new trajectory is then simulated from this point, both backward and forward in time until one of the states is reached. Being in a transition region, this will not take long. If the new path still connects A to B it is accepted, otherwise it is rejected and the procedure starts again.
Protein folding
Protein folding is the process by which a protein structure assumes its functional shape or conformation. It is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil....
, chemical reaction
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
s and nucleation
Nucleation
Nucleation is the extremely localized budding of a distinct thermodynamic phase. Some examples of phases that may form by way of nucleation in liquids are gaseous bubbles, crystals or glassy regions. Creation of liquid droplets in saturated vapor is also characterized by nucleation...
. Standard simulation tools such as molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
can generate the dynamical trajectories of all the atoms in the system. However, because of the time gap between simulations and reality, even present supercomputers would require years of simulations to show an event that occurs once a μs.
Transition path ensemble
TPS focuses on the most interesting part of the simulation, the transition. For example, an initially unfolded protein will vibrate for a long time in an open-string configuration before undergoing a transition and fold on itself. The aim of the method is to reproduce precisely those folding moments.Consider in general a system with two stable states A and B. The system will spend a long time in those states and occasionally jump from one to the other. There are many ways in which the transition can take place. Once a probability is assigned to each of the many pathways, one can construct a Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
random walk in the path space of the transition trajectories, and thus generate the ensemble of all transition paths. All the relevant information can then be extracted from the ensemble, such as the reaction mechanism, the transition states, and the rate constants.
Given an initial path, TPS provides some algorithms to perturb that path and create a new one. As in all Monte Carlo walks, the new path will then be accepted or rejected in order to have the correct path probability. The procedure is iterated and the ensemble is gradually sampled.
A powerful and efficient algorithm is the so-called shooting move. Consider the case of a classical many-body system described by coordinates r and momenta p. Molecular dynamics generates a path as a set of (rt, pt) at discrete times t in [0,T] where T is the length of the path. For a transition from A to B, (r0, p0) is in A, and (rT, pT) is in B. One of the path times is chosen at random, the momenta p are modified slightly into p + δp, where δp is a random perturbation consistent with system constraints, e.g. conservation of energy and linear and angular momentum. A new trajectory is then simulated from this point, both backward and forward in time until one of the states is reached. Being in a transition region, this will not take long. If the new path still connects A to B it is accepted, otherwise it is rejected and the procedure starts again.
Rate constant computation
In the Bennett–Chandler procedure the rate constant kAB for the transition from A to B is derived from the correlation function-
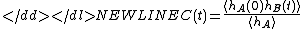
where hA(B) is the characteristic function of state A(B), and hA(B)(t) is either 1 if the system at time t is in state A(B) or 0 if not. The time-derivative C'(t) starts at time 0 at the transition state theoryTransition state theoryTransition state theory explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium between reactants and activated transition state complexes....
(TST) value kABTST and reaches a plateau kAB ≤ kABTST for times of the order of the transition time. Hence once the function is known up to these times, the rate constant is also available.
In the TPS framework C(t) can be rewritten as an average in the path ensemble
-

where the subscript AB denotes an average in the ensemble of paths that start in A and visit B. Time t is an arbitrary time in the plateau region of C(t). The factor C(t' ) at this specific time can be computed with a combination of path sampling and umbrella samplingUmbrella samplingUmbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977...
.
Transition interface sampling
The TPS rate constant calculation can be improved in a variation of the method called Transition interface sampling (TIS). In this method the transition region is divided in subregions using interfaces. The first interface defines state A and the last state B. The interfaces are not physical interfaces but hypersurfaces in the phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
The rate constant can be viewed as a flux through these interfaces. The rate kAB is the flux of trajectories starting before the first interface and going through the last interface. Being a rare event, the flux is very small and practically impossible to compute with a direct simulation. However, using the other interfaces between the states, one can rewrite the flux in terms of transition probabilities between interfaces
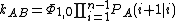
where PA(i + 1|i) is the probability for trajectories, coming from state A and crossing interface i, to reach interface i + 1. Here interface 0 defines state A and interface n defines state B. The factor Φ1,0 is the flux through the interface closest to A. By making this interface close enough, the quantity can be computed with a standard simulation, as the crossing event through this interface is not a rare event any more.
Remarkably, in the formula above there is no Markov assumption of independent transition probabilities. The quantities PA(i + 1|i) carry a subscript A to indicate that the probabilities are all dependent on the past history of the path, all the way from when it left A. These probabilities can be computed with a path sampling simulation using the TPS shooting move. A path crossing interface i is perturbed and a new path is shot. If the path still starts from A and crosses interface i, is accepted. The probability PA(i + 1|i) follows from the ratio of the number of paths that reach interface i + 1 to the total number of paths in the ensemble.
Theoretical considerations show that TIS computations are at least twice as fast as TPS, and computer experiments have shown that the TIS rate constant can converge up to 10 times faster. A reason for this is due to TIS using paths of adjustable length and on average shorter than TPS. Also, TPS relies on the correlation function C(t), computed by summation of positive and negative terms due to recrossings. TIS instead computes the rate as an effective positive flux, the quantity kAB is directly computed as an average of only positive terms contributing to the interface transition probabilities.
Stochastic process rare event sampling
TPS/TIS as normally implemented can be acceptable for non-equilibrium calculations provided that the interfacial fluxes are time-independent (stationaryStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
). To treat non-stationary systems in which there is time dependence in the dynamics, due either to variation of an external parameter or to evolution of the system itself, then the scheme for branching paths must be altered so as to achieve information which is distributed evenly in time and which takes account of changing fluxes through different regions of the phase space.
Instead of branching at each instance of crossing an interface, the S-PRES algorithm (Stochastic Process Rare Event Sampling) branches paths at fixed time intervals, with the degree of branching or pruning determined in a manner similar to the Pruned-Enriched Rosenbluth Sampling technique such that the probability of selecting a configuration as the starting point for a new path segment is conditioned jointly by its probability of appearing in an unbiased simulation and by its position relative to the ordered sequence of transition interfaces. This allows ready observation of rare events with respect to time. An additional benefit relative to conventional TPS and TIS is that over most of the phase space the reaction coordinate only needs to be evaluated at fixed time intervals (rather than continuously) because the exact timepoint at which interfaces other than the final interface n are reached is no longer of importance.
External links
- C++ source code of an S-PRES wrapper program, with optional parallelism using OpenMPOpenMPOpenMP is an API that supports multi-platform shared memory multiprocessing programming in C, C++, and Fortran, on most processor architectures and operating systems, including Linux, Unix, AIX, Solaris, Mac OS X, and Microsoft Windows platforms...
.
- C++ source code of an S-PRES wrapper program, with optional parallelism using OpenMP
-

