
Translation plane
Encyclopedia
In mathematics
, a translation plane is a particular kind of projective plane
, as considered as a combinatorial object.
In a projective plane, represents a point, and
represents a point, and  represents a line. A central collineation
represents a line. A central collineation
with center and axis
and axis  is a collineation fixing every point on
is a collineation fixing every point on  and every line through
and every line through  . It is called an "elation" if
. It is called an "elation" if  is on
is on  , otherwise it is called a "homology". The central collineations with centre
, otherwise it is called a "homology". The central collineations with centre  and axis
and axis  form a group.
form a group.
A projective plane is called a translation plane if there exists a line
is called a translation plane if there exists a line  such that the group of elations with axis
such that the group of elations with axis  is transitive on the affine plane Πl (the affine
is transitive on the affine plane Πl (the affine
derivative of Π).
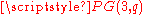 is a set of q2 + 1 lines, with no two intersecting. Equivalently, it is a partition of the points of
is a set of q2 + 1 lines, with no two intersecting. Equivalently, it is a partition of the points of 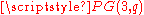 into lines.
into lines.
Given a spread of
of 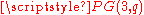 , the André/Bruck-Bose construction1 produces a translation plane
, the André/Bruck-Bose construction1 produces a translation plane 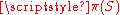 of order q2 as follows: Embed
of order q2 as follows: Embed 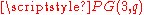 as a hyperplane of
as a hyperplane of 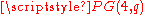 . Define an incidence structure
. Define an incidence structure  with "points," the points of
with "points," the points of 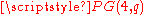 not on
not on 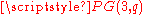 and "lines" the planes of
and "lines" the planes of 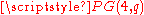 meeting
meeting  in a line of
in a line of  . Then
. Then  is a translation affine plane of order q2. Let
is a translation affine plane of order q2. Let 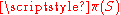 be the projective completion of
be the projective completion of  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a translation plane is a particular kind of projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, as considered as a combinatorial object.
In a projective plane,
 represents a point, and
represents a point, and  represents a line. A central collineation
represents a line. A central collineationCollineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
with center
 and axis
and axis  is a collineation fixing every point on
is a collineation fixing every point on  and every line through
and every line through  . It is called an "elation" if
. It is called an "elation" if  is on
is on  , otherwise it is called a "homology". The central collineations with centre
, otherwise it is called a "homology". The central collineations with centre  and axis
and axis  form a group.
form a group.A projective plane
 is called a translation plane if there exists a line
is called a translation plane if there exists a line  such that the group of elations with axis
such that the group of elations with axis  is transitive on the affine plane Πl (the affine
is transitive on the affine plane Πl (the affineAffine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
derivative of Π).
Relationship to spreads
Translation planes are related to spreads in finite projective spaces by the André/Bruck-Bose construction. A spread of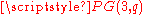 is a set of q2 + 1 lines, with no two intersecting. Equivalently, it is a partition of the points of
is a set of q2 + 1 lines, with no two intersecting. Equivalently, it is a partition of the points of 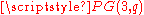 into lines.
into lines.Given a spread
 of
of 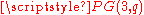 , the André/Bruck-Bose construction1 produces a translation plane
, the André/Bruck-Bose construction1 produces a translation plane 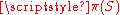 of order q2 as follows: Embed
of order q2 as follows: Embed 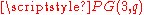 as a hyperplane of
as a hyperplane of 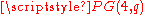 . Define an incidence structure
. Define an incidence structure  with "points," the points of
with "points," the points of 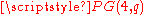 not on
not on 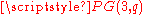 and "lines" the planes of
and "lines" the planes of 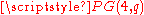 meeting
meeting  in a line of
in a line of  . Then
. Then  is a translation affine plane of order q2. Let
is a translation affine plane of order q2. Let 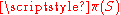 be the projective completion of
be the projective completion of  .
.
