
Tree of primitive Pythagorean triples
Encyclopedia
In mathematics, a Pythagorean triple
is a set of three positive integer
s a, b, and c having the property that they can be respectively the two legs and the hypotenuse
of a right triangle
, thus satisfying the equation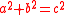 ; the triple is said to be primitive if and only if
; the triple is said to be primitive if and only if
a, b, and c share no common divisor
. The set of all primitive Pythagorean triples has the structure of a rooted tree
, specifically a ternary tree
, in a natural way. This may have been first discovered by B. Berggren in 1934.
F. J. M. Barning showed that when any of the three matrices
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
is a set of three positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a, b, and c having the property that they can be respectively the two legs and the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
, thus satisfying the equation
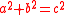 ; the triple is said to be primitive if and only if
; the triple is said to be primitive if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a, b, and c share no common divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
. The set of all primitive Pythagorean triples has the structure of a rooted tree
Tree structure
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
, specifically a ternary tree
Ternary tree
In computer science, a ternary tree is a tree data structure in which each node has at most three child nodes, usually distinguished as "left", “mid” and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a...
, in a natural way. This may have been first discovered by B. Berggren in 1934.
F. J. M. Barning showed that when any of the three matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
-
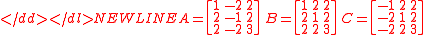
is multipliedMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
on the right by a column vector whose components form a Pythagorean triple, then the result is another column vector whose components are a different Pythagorean triple. If the initial triple is primitive, then so is the one that results. Thus each primitive Pythagorean triple has three "children". All primitive Pythagorean triples are descended in this way from the triple (3 ,4, 5), and no primitive triple appears more than once. The result may be graphically represented as a infinite ternary tree with (3, 4, 5) at the root node (see classic tree at right). This tree also appeared in papers of A. Hall in 1970 and A. R. Kanga in 1990.
Properties
The transformation using matrix A, if performed repeatedly from (a, b, c) = (3, 4, 5), preserves the feature b + 1 = c; matrix B preserves a – b = ±1 starting from (3, 4, 5); and matrix C preserves the feature a + 2 = c starting from (3, 4, 5).
A geometric interpretation for this tree involves the excircles present at each node. The three children of any parent triangle “inherit” their inradii from the parent: the parent’s excircle radii become the inradii for the next generation. For example, parent ( 3, 4, 5) has excircle radii equal to 2, 3, and 6. These are precisely the inradii of the three children (5, 12, 13), (15, 8, 17) and respectively.
If either of A or C is applied repeatedly from any Pythagorean triple used as an initial condition, then the dynamics of any of a, b, and c can be expressed as the dynamics of x in
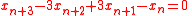
which is patterned on the matrices' shared characteristic equation

If B is applied repeatedly, then the dynamics of any of a, b, and c can be expressed as the dynamics of x in
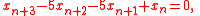
which is patterned on the characteristic equation of B.
Moreover, an infinitude of other third-order univariate difference equations can be found by multiplying any of the three matrices together an arbitrary number of times in an arbitrary sequence. For instance, the matrix D = CB moves one out the tree by two nodes (across, then down) in a single step; the characteristic equation of D provides the pattern for the third-order dynamics of any of a, b, or c in the non-exhaustive tree formed by D.
Alternative methods of generating the tree
Another approach to the dynamics of this tree relies on the standard formula for generating all primitive Pythagorean triples:
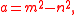

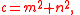
with m > n > 0 and m and n coprime and of opposite parity. Pairs (m, n) can be iterated by pre-multiplying them (expressed as a column vector) by any of

each of which preserves the inequalities, coprimeness, and opposite parity. The resulting ternary tree contains every such (m, n) pair exactly once, and when converted into (a, b, c) triples it becomes identical to the tree described above.
Another way of using two underlying parameters to generate the tree of triples uses an alternative formula for all primitive triples:

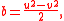
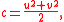
with u > v > 0 and u and v coprime and both odd. Pairs (u, v) can be iterated by pre-multiplying them (expressed as a column vector) by any of the above 2 × 2 matrices, all three of which preserve the inequalities, coprimeness, and the odd parity of both elements. When this process is begun at (3, 1), the resulting ternary tree contains every such (u, v) pair exactly once, and when converted into (a, b, c) triples it becomes identical to the tree described above.
A different tree
A different tree found by Price may be produced in a similar way using matrices A',B',C' shown below. (See Pythagorean triples by use of matrices and linear transformations.)
-
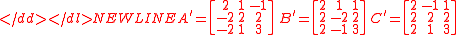
External links
- The Trinary Tree(s) underlying Primitive Pythagorean Triples at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- The Trinary Tree(s) underlying Primitive Pythagorean Triples at cut-the-knot
-

