
Trichotomy
Encyclopedia
In mathematics, the Law of Trichotomy states that every real number is either positive, negative, or zero. More generally, trichotomy is the property of an order relation < on a set X that for any x and y, exactly one of the following holds:  ,
,  , or
, or  .
.
In mathematical notation
, this is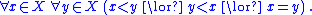
In classical logic, this axiom of trichotomy holds for ordinary comparison between real number
s and therefore also for comparisons between integer
s and between rational number
s.
In ZF set theory
, the law of trichotomy holds between cardinal number
s if and only if the axiom of choice holds.
More generally, a binary relation
R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x=y holds. If such a relation is also transitive
it is a strict total order; this is a special case of a strict weak order. For example, in the case of three element set {a,b,c} the relation R given by aRb, aRc, bRc is a strict total order, while the relation R given by the cyclic aRb, bRc, cRa is a non-transitive trichotomous relation.
In the definition of an ordered integral domain or ordered field
, the law of trichotomy is usually taken as more foundational than the law of total order
.
Trichotomous relations cannot be reflexive
, since xRx must be false. If transitive, they are trivially antisymmetric and also asymmetric, since xRy and yRx cannot both hold.
 ,
,  , or
, or  .
.In mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
, this is
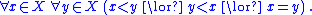
In classical logic, this axiom of trichotomy holds for ordinary comparison between real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and therefore also for comparisons between integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and between rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s.
In ZF set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, the law of trichotomy holds between cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s if and only if the axiom of choice holds.
More generally, a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x=y holds. If such a relation is also transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
it is a strict total order; this is a special case of a strict weak order. For example, in the case of three element set {a,b,c} the relation R given by aRb, aRc, bRc is a strict total order, while the relation R given by the cyclic aRb, bRc, cRa is a non-transitive trichotomous relation.
In the definition of an ordered integral domain or ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, the law of trichotomy is usually taken as more foundational than the law of total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
Trichotomous relations cannot be reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, since xRx must be false. If transitive, they are trivially antisymmetric and also asymmetric, since xRy and yRx cannot both hold.

