Trigonometric moment problem
Encyclopedia
In mathematics
, the trigonometric moment problem is formulated as follows: given a finite sequence {α0, ... αn }, does there exist a positive Borel measure μ on the interval [0, 2π] such that
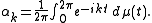
In other words, an affirmative answer to the problems means that {α0, ... αn } are the first n + 1 Fourier coefficients of some positive Borel measure μ on [0, 2π].
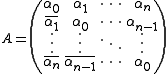
is positive semidefinite
.
The "only if" part of the claims can be verified by a direct calculation.
We sketch an argument for the converse. The positive semidefinite matrix A defines a sesquilinear product on Cn + 1, resulting in a Hilbert space
of dimensional at most n + 1, a typical element of which is an equivalence class denoted by [f]. The Toeplitz structure of A means that a "truncated" shift is a partial isometry
on
. More specifically, let { e0, ...en } be the standard basis of Cn + 1. Let 
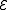be the subspace generated by { [e0], ... [en - 1] } and 
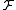be the subspace generated by { [e1], ... [en] }. Define an operator
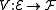
by
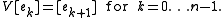
Since
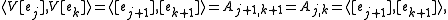
V can be extended to a partial isometry acting on all of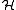
. Take a minimal unitary
extension U of V, on a possibly larger space (this always exists). According to the spectral theorem
, there exists a Borel measure m on the unit circle T such that for all integer k
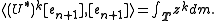
For k = 0,...,n, the left hand side is
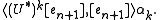
Finally, parametrize the unit circle T by eit on [0, 2π] gives
for some suitable measure μ.
V.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the trigonometric moment problem is formulated as follows: given a finite sequence {α0, ... αn }, does there exist a positive Borel measure μ on the interval [0, 2π] such that
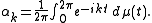
In other words, an affirmative answer to the problems means that {α0, ... αn } are the first n + 1 Fourier coefficients of some positive Borel measure μ on [0, 2π].
Characterization
The trigonometric moment problem is solvable, that is, {αk} is a sequence of Fourier coefficients, if and only if the (n + 1) × (n + 1) Toeplitz matrixToeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
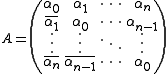
is positive semidefinite
Positive semidefinite
In mathematics, positive semidefinite may refer to:* positive-semidefinite matrix* positive-semidefinite function...
.
The "only if" part of the claims can be verified by a direct calculation.
We sketch an argument for the converse. The positive semidefinite matrix A defines a sesquilinear product on Cn + 1, resulting in a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of dimensional at most n + 1, a typical element of which is an equivalence class denoted by [f]. The Toeplitz structure of A means that a "truncated" shift is a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
on
. More specifically, let { e0, ...en } be the standard basis of Cn + 1. Let 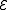be the subspace generated by { [e0], ... [en - 1] } and 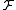be the subspace generated by { [e1], ... [en] }. Define an operator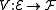by
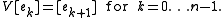
Since
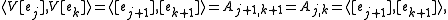
V can be extended to a partial isometry acting on all of
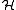. Take a minimal unitaryUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
extension U of V, on a possibly larger space (this always exists). According to the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, there exists a Borel measure m on the unit circle T such that for all integer k
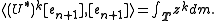
For k = 0,...,n, the left hand side is
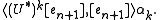
Finally, parametrize the unit circle T by eit on [0, 2π] gives
for some suitable measure μ.
Parametrization of solutions
The above discussion shows that the trigonometric moment problem has infinitely many solutions if the Toeplitz matrix A is invertible. In that case, the solutions to the problem are in bijective correspondence with minimal unitary extensions of the partial isometryPartial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
V.