Trilateration
Encyclopedia
In geometry
, trilateration is the process of determinating absolute or relative locations of points by measurement of distances, using the geometry of circles, sphere
s or triangle
s. In addition to its interest as a geometric problem, trilateration does have practical applications in surveying
and navigation
, including global positioning system
s (GPS). In contrast to triangulation
it does not involve the measurement of angle
s.
In two-dimensional geometry
, when it is known that a point lies on two curves such as the boundaries of two circles then the circle centers and the two radii provide sufficient information to narrow the possible locations down to two. Additional information may narrow the possibilities down to one unique location.
In three-dimensional geometry, when it is known that a point lies on three surfaces such as the surfaces of three spheres then the centers of the three spheres along with their radii provide sufficient information to narrow the possible locations down to no more than two. If it is known that the point lies on the surface of a fourth sphere then knowledge of this sphere's center along with its radius is sufficient to determine the one unique location.
This article describes a method for determining the intersections of three sphere surfaces given the centers and radii of the three spheres.
.
We start with the equations for the three spheres:
We need to find a point located at (x, y, z) that satisfies all three equations.
First we subtract the second equation from the first and solve for x:
.
We assume that the first two spheres intersect in more than one point, that is that
.
In this case substituting the equation for x back into the equation for the first sphere produces the equation for a circle, the solution to the intersection of the first two spheres:
.
Substituting :
into the formula for the third sphere and solving for y there results:
.
Now that we have the x- and y-coordinates of the solution point, we can simply rearrange the formula for the first sphere to find the z-coordinate:
Now we have the solution to all three points x, y and z. Because z is expressed as the positive or negative square root, it is possible for there to be zero, one or two solutions to the problem.
This last part can be visualized as taking the circle found from intersecting the first and second sphere and intersecting that with the third sphere. If that circle falls entirely outside or inside of the sphere, z is equal to the square root of a negative number
: no real solution exists. If that circle touches the sphere on exactly one point, z is equal to zero. If that circle touches the surface of the sphere at two points, then z is equal to plus or minus the square root of a positive number.
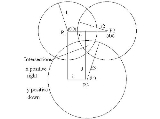
This problem can be overcome as described below where the points, P1, P2, and P3 are treated as vectors from the origin where indicated. P1, P2, and P3 are of course expressed in the original coordinate system.
is the unit vector in the direction from P1 to P2.
is the signed magnitude of the x component, in the figure 1 coordinate system, of the vector from P1 to P3.
is the unit vector in the y direction. Note that the points P1, P2, and P3 are all in the z=0 plane of the figure 1 coordinate system.
The third basis unit vector is
. Therefore,
the distance between the centers P1 and P2 and
is the signed magnitude of the y component, in the figure 1 coordinate system, of the vector from P1 to P3.
Using
as computed above, solve for x, y and z as described in the Derivation section. Then
gives the points in the original coordinate system since
, the basis unit vectors, are expressed in the original coordinate system.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, trilateration is the process of determinating absolute or relative locations of points by measurement of distances, using the geometry of circles, sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s or triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s. In addition to its interest as a geometric problem, trilateration does have practical applications in surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
and navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, including global positioning system
Global Positioning System
The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...
s (GPS). In contrast to triangulation
Triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
it does not involve the measurement of angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s.
In two-dimensional geometry
2D geometric model
A 2D geometric model is a geometric model of an object as two-dimensional figure, usually on the Euclidean or Cartesian plane.Even though all material objects are three-dimensional, a 2D geometric model is often adequate for certain flat objects, such as paper cut-outs and machine parts made of...
, when it is known that a point lies on two curves such as the boundaries of two circles then the circle centers and the two radii provide sufficient information to narrow the possible locations down to two. Additional information may narrow the possibilities down to one unique location.
In three-dimensional geometry, when it is known that a point lies on three surfaces such as the surfaces of three spheres then the centers of the three spheres along with their radii provide sufficient information to narrow the possible locations down to no more than two. If it is known that the point lies on the surface of a fourth sphere then knowledge of this sphere's center along with its radius is sufficient to determine the one unique location.
This article describes a method for determining the intersections of three sphere surfaces given the centers and radii of the three spheres.
Derivation
The intersections of the surfaces of three spheres is found by formulating the equations for the three sphere surfaces and then solving the three equations for the three unknowns, x, y, and z. To simplify the calculations, the equations are formulated so that the centers of the spheres are on the z=0 plane. Also the formulation is such that one center is at the origin, and one other is on the x-axis. It is possible to formulate the equations in this manner since any three non-colinear points lie on a unique plane. After finding the solution it can be transformed back to the original three dimensional Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
We start with the equations for the three spheres:
We need to find a point located at (x, y, z) that satisfies all three equations.
First we subtract the second equation from the first and solve for x:
.We assume that the first two spheres intersect in more than one point, that is that
.In this case substituting the equation for x back into the equation for the first sphere produces the equation for a circle, the solution to the intersection of the first two spheres:
.Substituting :
into the formula for the third sphere and solving for y there results:.Now that we have the x- and y-coordinates of the solution point, we can simply rearrange the formula for the first sphere to find the z-coordinate:
Now we have the solution to all three points x, y and z. Because z is expressed as the positive or negative square root, it is possible for there to be zero, one or two solutions to the problem.
This last part can be visualized as taking the circle found from intersecting the first and second sphere and intersecting that with the third sphere. If that circle falls entirely outside or inside of the sphere, z is equal to the square root of a negative number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
: no real solution exists. If that circle touches the sphere on exactly one point, z is equal to zero. If that circle touches the surface of the sphere at two points, then z is equal to plus or minus the square root of a positive number.
Preliminary and final computations
The section Derivation pointed out that the coordinate system in which the sphere centers are designated must be such that (1) all three centers are in the plane, Z = 0, (2) the sphere center, P1, is at the origin, and (3) the sphere center, P2, is on the X axis. In general the problem will not be given in a form such that these requirement are met.This problem can be overcome as described below where the points, P1, P2, and P3 are treated as vectors from the origin where indicated. P1, P2, and P3 are of course expressed in the original coordinate system.
is the unit vector in the direction from P1 to P2. is the signed magnitude of the x component, in the figure 1 coordinate system, of the vector from P1 to P3. is the unit vector in the y direction. Note that the points P1, P2, and P3 are all in the z=0 plane of the figure 1 coordinate system.The third basis unit vector is
. Therefore, the distance between the centers P1 and P2 and is the signed magnitude of the y component, in the figure 1 coordinate system, of the vector from P1 to P3.Using
as computed above, solve for x, y and z as described in the Derivation section. Thengives the points in the original coordinate system since
, the basis unit vectors, are expressed in the original coordinate system.See also
- Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
- MultilaterationMultilaterationMultilateration is a navigation technique based on the measurement of the difference in distance to two or more stations at known locations that broadcast signals at known times. Unlike measurements of absolute distance or angle, measuring the difference in distance results in an infinite number of...
- position estimation using measurements of time difference of arrival at (or from) three or more sites. - ResectionResection (orientation)Resection is a method for determining a position using a compass and topographic map .-Resection versus intersection:...
- TriangulationTriangulationIn trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
- Global positioning systemGlobal Positioning SystemThe Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...