In real algebraic geometry

Real algebraic geometry

In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....

, a general quartic plane curve

Quartic plane curve

A quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0....

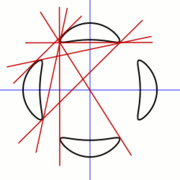
 has 28 bitangent

Bitangent

In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...

 lines, lines that are tangent to the curve in two places. These lines exist in the complex projective plane, but it is possible to define curves for which all 28 of these lines have real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s as their coordinates and therefore belong to the Euclidean plane.

An explicit quartic with twenty-eight real bitangents was first given by As Plücker showed, the number of real bitangents of any quartic must be 28, 16, or a number less than 9. Another quartic with 28 real bitangents can be formed by the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

 of centers of ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

s with fixed axis lengths, tangent to two non-parallel lines.
gave a different construction of a quartic with twenty-eight bitangents, formed by projecting a cubic surface

Cubic surface

A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...

; twenty-seven of the bitangents to Shioda's curve are real while the twenty-eighth is the line at infinity

Line at infinity

In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...

 in the projective plane.

Example

The Trott curve, another curve with 28 real bitangents, is the set of points (x,y) satisfying the degree

Degree of a polynomial

The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

 four polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

 equation
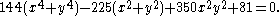
These points form a nonsingular quartic curve that has genus

Geometric genus

In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...

 three and that has twenty-eight real bitangent

Bitangent

In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...

s.

Like the examples of Plücker and of Blum and Guinand, the Trott curve has four separated ovals, the maximum number for a curve of degree four, and hence is an M-curve

Harnack's curve theorem

In real algebraic geometry, Harnack's curve theorem, named after Axel Harnack, describes the possible numbers of connected components that an algebraic curve can have, in terms of the degree of the curve...

. The four ovals can be grouped into six different pairs of ovals; for each pair of ovals there are four bitangents touching both ovals in the pair, two that separate the two ovals, and two that do not. Additionally, each oval bounds a nonconvex region of the plane and has one bitangent spanning the nonconvex portion of its boundary.

Connections to other structures

The dual curve

Dual curve

In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree...

 to a quartic curve has 28 real ordinary double points, dual to the 28 bitangents of the primal curve.

The 28 bitangents of a quartic may also be placed in correspondence with symbols of the form
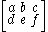
where a, b, c, d, e and f are all zero or one and where

ad + be + ef = 1 (mod 2).

There are 64 choices for a, b, c, d, e and f, but only 28 of these choices produce an odd sum. One may also interpret a, b, and c as the homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

 of a point of the Fano plane

Fano plane

In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...

 and d, e, and f as the coordinates of a line in the same finite projective plane; the condition that the sum is odd is equivalent to requiring that the point and the line do not touch each other, and there are 28 different pairs of a point and a line that do not touch. The points and lines of the Fano plane that are disjoint from a non-incident point-line pair form a triangle, and the bitangents of a quartic have been considered as being in correspondence with the 28 triangles of the Fano plane.

The 28 bitangents of a quartic also correspond to pairs of the 56 lines on a degree-2 del Pezzo surface

Del Pezzo surface

In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...

, and to the 28 odd theta characteristic

Theta characteristic

In mathematics, a theta characteristic of a non-singular algebraic curve C is a divisor class Θ such that 2Θ is the canonical class, In terms of holomorphic line bundles L on a connected compact Riemann surface, it is therefore L such that L2 is the canonical bundle, here also equivalently the...

s.

The 27 lines on the cubic and the 28 bitangents on a quartic, together with the 120 tritangent planes of a canonic sextic curve of genus 4, form a "trinity" in the sense of Vladimir Arnold

Vladimir Arnold

Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...

, specifically a form of McKay correspondence, and can be related to many further objects, including E₇ and E₈, as discussed at trinities.