
UNIQUAC
Encyclopedia
UNIQUAC is an activity coefficient
model used in description of phase equilibria.
The model is a so-called lattice model and has been derived from a first order approximation
of interacting molecule surfaces in statistical thermodynamics. The model is however not fully thermodynamically consistent due to its two liquid mixture approach. In this approach the local concentration around one central molecule is assumed to be independent from the local composition around another type of molecule.
It has been shown that while the local compositions are correlated, ignoring this correlation gives little effect on the correlation of activity coefficients. Today the UNIQUAC model is frequently applied in the description of phase equilibria (i.e. liquid–solid,liquid–liquid or liquid–vapor equilibrium). The UNIQUAC model also serves as the basis of the development of the group contribution method UNIFAC
, where molecules are subdivided in atomic groups. In fact, UNIQUAC is equal to UNIFAC for mixtures of molecules, which are not subdivided; e.g. the binary systems water-methanol, methanol-acryonitrile and formaldehyde-DMF.
A more thermodynamically consistent form of UNIQUAC is given by the more recent COSMOSPACE
and the equivalent GEQUAC model.
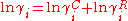
The first is an entropic term quantifying the deviation from ideal solubility as a result of differences in molecule shape. The latter is an enthalpic Here it is assumed that the enthalpy change upon mixing can be assumed to be equal to the energy upon mixing, since the liquid excess molar volume is small and Δ Hex=ΔUex+Vex ΔP ≈ ΔU correction caused by the change in interacting forces between different molecules upon mixing.
The excess entropy γC is calculated exclusively from the pure chemical parameters, using the relative Van der Waals volumes ri and surface areas qi of the pure chemicals.
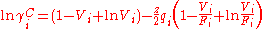
With the volume fraction per mixture mole fraction, Vi, for the ith
component given by:
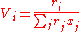
And the surface area fraction per mixture molar fraction, Fi, for the
ith component given by:
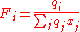
The first 3 terms on the right hand side of the combinatorial term form the Flory-Huggins contribution, while the left terms, the Guggenhem-Staverman correction, reduce this because the segments of a molecule are hindered. The coordination number, z, i.e. the number of close interacting molecules around a central molecule, is frequently set to 10. It can be regarded as an average value that lies between cubic (z=6) and hexagonal packing (z=12) of molecules that are simplified by spheres.
In the limit of infinite dilution and a binary mixture the equations for the combinatorial contribution reduces to:
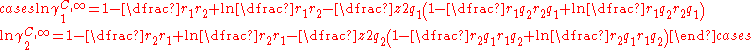
This pair of equation shows that molecules of same shape, i.e. same r and q parameters, have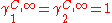
 , which is derived from
, which is derived from
experimental or occasionally estimated activity coefficients. The expression for the residual activity coefficient for molecule i is:

with

Δuij [J/mol] is the binary interaction energy parameter. Theory defines
Δuij = uij – uii, and Δuji = uji – ujj, where uij is the interaction energy between molecules i and j.
Usually Δuij ≠ Δuji, because the energies of evaporation (i.e. uii), are in may cases different, while the energy of interaction between molecule i and j is symmetric, and therefore uij=uji. If the interactions between the j molecules and i molecules is the same as between molecules i and j, than mixing has no excess energy effect upon mixing, Δuij=Δuji=0. And thus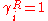
Alternatively, in some process simulation software can be expressed as follows :
can be expressed as follows :
 .
.
The "C", "D", and "E" coefficients are primarily used in fitting liquid–liquid equilibria (with "D" and "E" rarely used at that). The "C" coefficient is useful in vapor-liquid equilibria as well.
programs to calculate the mass balance in and around separation units.
Activity coefficient
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
model used in description of phase equilibria.
The model is a so-called lattice model and has been derived from a first order approximation
of interacting molecule surfaces in statistical thermodynamics. The model is however not fully thermodynamically consistent due to its two liquid mixture approach. In this approach the local concentration around one central molecule is assumed to be independent from the local composition around another type of molecule.
It has been shown that while the local compositions are correlated, ignoring this correlation gives little effect on the correlation of activity coefficients. Today the UNIQUAC model is frequently applied in the description of phase equilibria (i.e. liquid–solid,liquid–liquid or liquid–vapor equilibrium). The UNIQUAC model also serves as the basis of the development of the group contribution method UNIFAC
UNIFAC
The UNIversal Functional Activity Coefficient method is a semi-empirical system for the prediction of non-electrolyte activity estimation in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients...
, where molecules are subdivided in atomic groups. In fact, UNIQUAC is equal to UNIFAC for mixtures of molecules, which are not subdivided; e.g. the binary systems water-methanol, methanol-acryonitrile and formaldehyde-DMF.
A more thermodynamically consistent form of UNIQUAC is given by the more recent COSMOSPACE
COSMOSPACE
COSMOSPACE is an activity coefficient model in which the activity coefficient of the components in aliquid chemical mixture can be related through their molar fraction....
and the equivalent GEQUAC model.
Equations
In the UNIQUAC model the activity coefficients of the ith component of a two component mixture are described by a combinatorial and a residual contribution.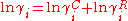
The first is an entropic term quantifying the deviation from ideal solubility as a result of differences in molecule shape. The latter is an enthalpic Here it is assumed that the enthalpy change upon mixing can be assumed to be equal to the energy upon mixing, since the liquid excess molar volume is small and Δ Hex=ΔUex+Vex ΔP ≈ ΔU correction caused by the change in interacting forces between different molecules upon mixing.
Combinatorial contribution
The combinatorial contribution accounts for shape differences between molecules and affects the entropy of the mixture and is based on the lattice theory.The excess entropy γC is calculated exclusively from the pure chemical parameters, using the relative Van der Waals volumes ri and surface areas qi of the pure chemicals.
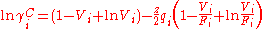
With the volume fraction per mixture mole fraction, Vi, for the ith
component given by:
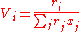
And the surface area fraction per mixture molar fraction, Fi, for the
ith component given by:
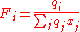
The first 3 terms on the right hand side of the combinatorial term form the Flory-Huggins contribution, while the left terms, the Guggenhem-Staverman correction, reduce this because the segments of a molecule are hindered. The coordination number, z, i.e. the number of close interacting molecules around a central molecule, is frequently set to 10. It can be regarded as an average value that lies between cubic (z=6) and hexagonal packing (z=12) of molecules that are simplified by spheres.
In the limit of infinite dilution and a binary mixture the equations for the combinatorial contribution reduces to:
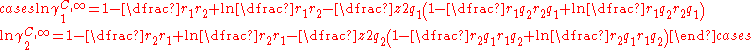
This pair of equation shows that molecules of same shape, i.e. same r and q parameters, have
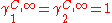
Residual contribution
The residual term contains an empirical parameter, , which is derived from
, which is derived fromexperimental or occasionally estimated activity coefficients. The expression for the residual activity coefficient for molecule i is:

with

Δuij [J/mol] is the binary interaction energy parameter. Theory defines
Δuij = uij – uii, and Δuji = uji – ujj, where uij is the interaction energy between molecules i and j.
Usually Δuij ≠ Δuji, because the energies of evaporation (i.e. uii), are in may cases different, while the energy of interaction between molecule i and j is symmetric, and therefore uij=uji. If the interactions between the j molecules and i molecules is the same as between molecules i and j, than mixing has no excess energy effect upon mixing, Δuij=Δuji=0. And thus
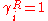
Alternatively, in some process simulation software
 can be expressed as follows :
can be expressed as follows : .
.The "C", "D", and "E" coefficients are primarily used in fitting liquid–liquid equilibria (with "D" and "E" rarely used at that). The "C" coefficient is useful in vapor-liquid equilibria as well.
Applications
Activity coefficients can be used to predict simple phase equilibria (vapour–liquid, liquid–liquid, solid–liquid), or to estimate other physical properties (e.g. viscosity of mixtures). Models such as UNIQUAC allow chemical engineers to predict the phase behavior of multicomponent chemical mixtures. They are commonly used in process simulationProcess simulation
Process simulation is used for the design, development, analysis, and optimization of technical processes and is mainly applied to chemical plants and chemical processes, but also to power stations, and similar technical facilities.- Main principle :...
programs to calculate the mass balance in and around separation units.
Parameters
UNIQUAC requires two basic underlying parameters:- Relative surface and volume fractions are chemical constants, which must be known for all chemicals.
- An empirical parameter between components that describes the intermolecular behaviour. This parameter must be known for all binary pairs in the mixture. In a quaternary mixture there are six such parameters (1–2,1–3,1–4,2–3,2–4,3–4) and the number rapidly increases with additional chemical components. The empirical parameters are derived from experimental activity coefficients, or from phase diagrams, from which the activity coefficients themselves can be calculated. An alternative is to obtain activity coefficients with a method such as UNIFACUNIFACThe UNIversal Functional Activity Coefficient method is a semi-empirical system for the prediction of non-electrolyte activity estimation in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients...
, and the UNIFAC parameters can then be simplified by fitting to obtain the UNIQUAC parameters. This method allows for the more rapid calculation of activity coefficients, rather than direct usage of the more complex method.
Newer developments
UNIQUAC has been extended by several research groups. Some selected derivatives are:- UNIFACUNIFACThe UNIversal Functional Activity Coefficient method is a semi-empirical system for the prediction of non-electrolyte activity estimation in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients...
: A method which permits the volume, surface and in particular,the binary interaction parameters to be estimated. This eliminates the use of experimental data to calculate the UNIQUAC parameters. - Extensions for the estimation of activity coefficients for electrolytic mixtures.
- Extensions for better describing the temperature dependence of activity coefficients
- Solutions for specific molecular arrangements.
See also
- Chemical equilibriumChemical equilibriumIn a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
- Chemical thermodynamicsChemical thermodynamicsChemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics...
- FugacityFugacityIn chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
- MOSCEDMOSCEDMOSCED is a thermodynamic model for the estimation of limiting activity coefficients . From a historical point of view MOSCED can be regarded as an improved modification of the Hansen method and the Hildebrand solubility model...
, a model for estimating limiting activity coefficients at infinite dilution - NRTL, an alternative to UNIQUAC of the same local composition type

