Ultraparallel theorem
Encyclopedia
In hyperbolic geometry
, the ultraparallel theorem states that every pair of ultraparallel lines in the hyperbolic plane
has a unique common perpendicular
hyperbolic line.
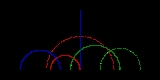
 Let
Let

be four distinct points on the abscissa
of the Cartesian plane. Let and
and  be semicircle
be semicircle
s above the abscissa with diameters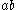 and
and 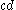 respectively. Then in the Poincaré half-plane model
respectively. Then in the Poincaré half-plane model
HP,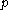 and
and  represent ultraparallel lines.
represent ultraparallel lines.
Compose the following two hyperbolic motion
s:
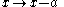
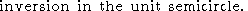
Then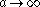 ,
, 
Now continue with these two hyperbolic motions: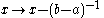
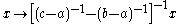
Then stays at
stays at  ,
, 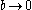 ,
, 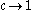 ,
, 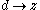 (say). The unique semicircle, with center at the origin, perpendicular to the one on
(say). The unique semicircle, with center at the origin, perpendicular to the one on 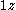 must have a radius tangent to the radius of the other. The right triangle formed by the abscissa and the perpendicular radii has hypotenuse of length
must have a radius tangent to the radius of the other. The right triangle formed by the abscissa and the perpendicular radii has hypotenuse of length 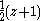 . Since
. Since 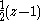 is the radius of the semicircle on
is the radius of the semicircle on 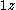 , the common perpendicular sought has radius-square
, the common perpendicular sought has radius-square
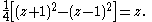
The four hyperbolic motions that produced above can each be inverted and applied in reverse order to the semicircle centered at the origin and of radius
above can each be inverted and applied in reverse order to the semicircle centered at the origin and of radius 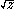 to yield the unique hyperbolic line perpendicular to both ultraparallels
to yield the unique hyperbolic line perpendicular to both ultraparallels  and
and 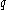 .
.
of the hyperbolic plane, two ultraparallel lines correspond to two non-intersecting chords. The poles
of these two lines are the respective intersections of the tangent lines to the unit circle
at the endpoints of the chords. Lines perpendicular to line A are modeled by chords whose extension passes through the pole of A. Hence we draw the unique line between the poles of the two given lines, and intersect it with the unit disk; the chord of intersection will be the desired common perpendicular of the ultraparallel lines. If one of the chords happens to be a diameter, we do not have a pole, but in this case any chord perpendicular to the diameter is perpendicular as well in the hyperbolic plane, and so we draw a line through the pole of the other line intersecting the diameter at right angles to get the common perpendicular.
The proof is completed by showing this construction is always possible. If both chords are diameters, they intersect. If only one of the chords is a diameter, the other chord projects orthogonally down to a section of the first chord contained in its interior, and a line from the pole orthogonal to the diameter intersects both the diameter and the chord. If both lines are not diameters, the we may extend the tangents drawn from each pole to produce a quadrilateral
with the unit circle inscribed within it. The poles are opposite vertices of this quadrilateral, and the chords are lines drawn between adjacent sides of the vertex, across opposite corners. Since the quadrilateral is convex, the line between the poles intersects both of the chords drawn across the corners, and the segment of the line between the chords defines the required chord perpendicular to the two other chords.
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, the ultraparallel theorem states that every pair of ultraparallel lines in the hyperbolic plane
Hyperbolic plane
In mathematics, the term hyperbolic plane may refer to:* A two-dimensional plane in hyperbolic geometry* A two-dimensional plane in Minkowski space...
has a unique common perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
hyperbolic line.
Proof in the Poincaré half-plane model


be four distinct points on the abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
of the Cartesian plane. Let
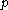 and
and 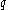 be semicircle
be semicircleSemicircle
In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...
s above the abscissa with diameters
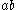 and
and 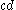 respectively. Then in the Poincaré half-plane model
respectively. Then in the Poincaré half-plane modelPoincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
HP,
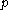 and
and  represent ultraparallel lines.
represent ultraparallel lines.Compose the following two hyperbolic motion
Hyperbolic motion
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program...
s:
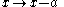
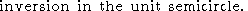
Then
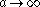 ,
, 
Now continue with these two hyperbolic motions:
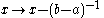
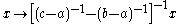
Then
 stays at
stays at  ,
, 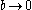 ,
, 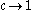 ,
, 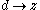 (say). The unique semicircle, with center at the origin, perpendicular to the one on
(say). The unique semicircle, with center at the origin, perpendicular to the one on 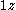 must have a radius tangent to the radius of the other. The right triangle formed by the abscissa and the perpendicular radii has hypotenuse of length
must have a radius tangent to the radius of the other. The right triangle formed by the abscissa and the perpendicular radii has hypotenuse of length 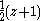 . Since
. Since 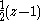 is the radius of the semicircle on
is the radius of the semicircle on 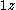 , the common perpendicular sought has radius-square
, the common perpendicular sought has radius-square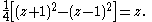
The four hyperbolic motions that produced
 above can each be inverted and applied in reverse order to the semicircle centered at the origin and of radius
above can each be inverted and applied in reverse order to the semicircle centered at the origin and of radius 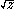 to yield the unique hyperbolic line perpendicular to both ultraparallels
to yield the unique hyperbolic line perpendicular to both ultraparallels  and
and 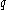 .
.Proof in the Klein model
In the Klein modelKlein model
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
of the hyperbolic plane, two ultraparallel lines correspond to two non-intersecting chords. The poles
Pole and polar
In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
of these two lines are the respective intersections of the tangent lines to the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
at the endpoints of the chords. Lines perpendicular to line A are modeled by chords whose extension passes through the pole of A. Hence we draw the unique line between the poles of the two given lines, and intersect it with the unit disk; the chord of intersection will be the desired common perpendicular of the ultraparallel lines. If one of the chords happens to be a diameter, we do not have a pole, but in this case any chord perpendicular to the diameter is perpendicular as well in the hyperbolic plane, and so we draw a line through the pole of the other line intersecting the diameter at right angles to get the common perpendicular.
The proof is completed by showing this construction is always possible. If both chords are diameters, they intersect. If only one of the chords is a diameter, the other chord projects orthogonally down to a section of the first chord contained in its interior, and a line from the pole orthogonal to the diameter intersects both the diameter and the chord. If both lines are not diameters, the we may extend the tangents drawn from each pole to produce a quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
with the unit circle inscribed within it. The poles are opposite vertices of this quadrilateral, and the chords are lines drawn between adjacent sides of the vertex, across opposite corners. Since the quadrilateral is convex, the line between the poles intersects both of the chords drawn across the corners, and the segment of the line between the chords defines the required chord perpendicular to the two other chords.

