
Unconditional convergence
Encyclopedia
In mathematical analysis
, a series
 in a Banach space
in a Banach space
X is unconditionally convergent if for every permutation
 the series
the series 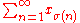 converges.
converges.
This notion is often defined in an equivalent way: A series is unconditionally convergent if for every sequence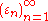 , with
, with 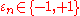 , the series
, the series
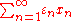
converges.
Every absolutely convergent
series is unconditionally convergent, but the converse
implication does not hold in general. When X = Rn, then, by the Riemann series theorem, the series is unconditionally convergent if and only if it is absolutely convergent.
is unconditionally convergent if and only if it is absolutely convergent.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
 in a Banach space
in a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X is unconditionally convergent if for every permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
 the series
the series 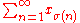 converges.
converges.This notion is often defined in an equivalent way: A series is unconditionally convergent if for every sequence
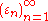 , with
, with 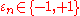 , the series
, the series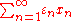
converges.
Every absolutely convergent
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
series is unconditionally convergent, but the converse
Converse (logic)
In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
implication does not hold in general. When X = Rn, then, by the Riemann series theorem, the series
 is unconditionally convergent if and only if it is absolutely convergent.
is unconditionally convergent if and only if it is absolutely convergent.

