
Unfolding
Encyclopedia
In mathematics, an unfolding of a function
is a certain family of functions.
Let be a smooth manifold and consider a smooth mapping
be a smooth manifold and consider a smooth mapping 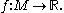 Let us assume that for given
Let us assume that for given 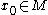 and
and 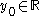 we have
we have 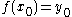 . Let
. Let 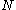 be a smooth
be a smooth 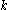 -dimensional manifold, and consider the family of mapping (parameterised by
-dimensional manifold, and consider the family of mapping (parameterised by 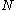 ) given by
) given by 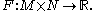 We say that
We say that  is a
is a 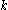 -parameter unfolding of
-parameter unfolding of  if
if 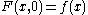 for all
for all 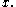 In other words the functions
In other words the functions 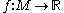 and
and 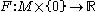 are the same: the function
are the same: the function 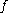 is contained in , or is unfolded by, the family
is contained in , or is unfolded by, the family 
Let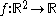 be given by
be given by 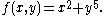 An example of an unfolding of
An example of an unfolding of  would be
would be 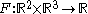 given by
given by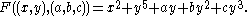
As is the case with unfoldings, and
and 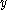 are called variables and
are called variables and 
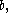 and
and  are called parameters - since they parameterise the unfolding.
are called parameters - since they parameterise the unfolding.
In practice we require that the unfoldings have certain nice properties. In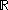 notice that
notice that  is a smooth mapping from
is a smooth mapping from 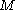 to
to 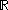 and so belongs to the function space
and so belongs to the function space
 As we vary the parameters of the unfolding we get different elements of the function space. Thus, the unfolding induces a function
As we vary the parameters of the unfolding we get different elements of the function space. Thus, the unfolding induces a function 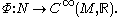 The space
The space  where
where  denotes the group
denotes the group
of diffeomorphism
s of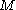 etc, acts
etc, acts
on The action is given by
The action is given by 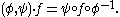 If
If 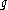 lies in the orbit of
lies in the orbit of 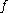 under this action then there is a diffeomorphic change of coordinates in
under this action then there is a diffeomorphic change of coordinates in 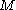 and
and 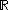 which takes
which takes 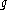 to
to  (and vice versa). One nice property that we may like to impose is that
(and vice versa). One nice property that we may like to impose is that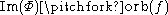
where " " denotes "transverse to". This property ensures that as we vary the unfolding parameters we can predict - by knowing how the orbit foliate
" denotes "transverse to". This property ensures that as we vary the unfolding parameters we can predict - by knowing how the orbit foliate
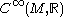 - how the resulting functions will vary.
- how the resulting functions will vary.
There is an idea of a versal unfolding. Every versal unfolding has the property that
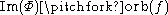 , but the converse is false. Let
, but the converse is false. Let 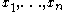 be local coordinates on
be local coordinates on 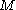 , and let
, and let 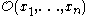 denote the ring
denote the ring
of smooth functions. We define the Jacobian ideal of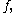 denoted by
denoted by 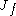 as follows:
as follows: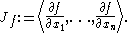
Then a basis for a versal unfolding of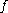 is given by quotient
is given by quotient

This quotient is known as the local algebra of The dimension of the local algebra is called the Milnor number of
The dimension of the local algebra is called the Milnor number of 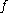 . The minimum number of unfolding parameters for a versal unfolding is equal to the Milnor number; that is not to say that every unfolding with that many parameters will be versal! Consider the function
. The minimum number of unfolding parameters for a versal unfolding is equal to the Milnor number; that is not to say that every unfolding with that many parameters will be versal! Consider the function  A calculation shows that
A calculation shows that
This means that give a basis for a versal unfolding, and that
give a basis for a versal unfolding, and that
is a versal unfolding. A versal unfolding with the minimum possible number of unfolding parameters is called a miniversal unfolding.
Sometimes unfoldings are called deformations, versal unfoldings are called versal deformations, etc.
An important object associated to an unfolding is its bifurcation set. This set lives in the parameter space of the unfolding, and gives all parameter values for which the resulting function has degenerate singularities.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is a certain family of functions.
Let
 be a smooth manifold and consider a smooth mapping
be a smooth manifold and consider a smooth mapping 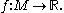 Let us assume that for given
Let us assume that for given 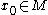 and
and 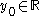 we have
we have 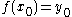 . Let
. Let 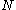 be a smooth
be a smooth 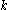 -dimensional manifold, and consider the family of mapping (parameterised by
-dimensional manifold, and consider the family of mapping (parameterised by 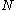 ) given by
) given by 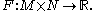 We say that
We say that  is a
is a 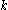 -parameter unfolding of
-parameter unfolding of  if
if 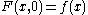 for all
for all 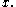 In other words the functions
In other words the functions 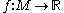 and
and 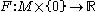 are the same: the function
are the same: the function 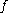 is contained in , or is unfolded by, the family
is contained in , or is unfolded by, the family 
Let
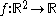 be given by
be given by 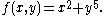 An example of an unfolding of
An example of an unfolding of  would be
would be 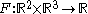 given by
given by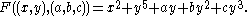
As is the case with unfoldings,
 and
and 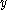 are called variables and
are called variables and 
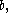 and
and  are called parameters - since they parameterise the unfolding.
are called parameters - since they parameterise the unfolding.In practice we require that the unfoldings have certain nice properties. In
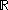 notice that
notice that  is a smooth mapping from
is a smooth mapping from 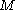 to
to 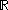 and so belongs to the function space
and so belongs to the function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
 As we vary the parameters of the unfolding we get different elements of the function space. Thus, the unfolding induces a function
As we vary the parameters of the unfolding we get different elements of the function space. Thus, the unfolding induces a function 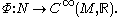 The space
The space  where
where  denotes the group
denotes the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of
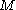 etc, acts
etc, actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on
 The action is given by
The action is given by 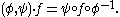 If
If 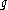 lies in the orbit of
lies in the orbit of 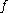 under this action then there is a diffeomorphic change of coordinates in
under this action then there is a diffeomorphic change of coordinates in 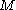 and
and 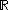 which takes
which takes 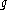 to
to  (and vice versa). One nice property that we may like to impose is that
(and vice versa). One nice property that we may like to impose is that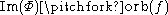
where "
 " denotes "transverse to". This property ensures that as we vary the unfolding parameters we can predict - by knowing how the orbit foliate
" denotes "transverse to". This property ensures that as we vary the unfolding parameters we can predict - by knowing how the orbit foliateFoliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
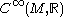 - how the resulting functions will vary.
- how the resulting functions will vary.There is an idea of a versal unfolding. Every versal unfolding has the property that
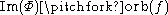 , but the converse is false. Let
, but the converse is false. Let 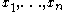 be local coordinates on
be local coordinates on 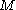 , and let
, and let 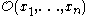 denote the ring
denote the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of smooth functions. We define the Jacobian ideal of
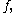 denoted by
denoted by 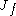 as follows:
as follows: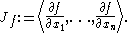
Then a basis for a versal unfolding of
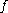 is given by quotient
is given by quotientQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...

This quotient is known as the local algebra of
 The dimension of the local algebra is called the Milnor number of
The dimension of the local algebra is called the Milnor number of 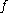 . The minimum number of unfolding parameters for a versal unfolding is equal to the Milnor number; that is not to say that every unfolding with that many parameters will be versal! Consider the function
. The minimum number of unfolding parameters for a versal unfolding is equal to the Milnor number; that is not to say that every unfolding with that many parameters will be versal! Consider the function  A calculation shows that
A calculation shows that
This means that
 give a basis for a versal unfolding, and that
give a basis for a versal unfolding, and that
is a versal unfolding. A versal unfolding with the minimum possible number of unfolding parameters is called a miniversal unfolding.
Sometimes unfoldings are called deformations, versal unfoldings are called versal deformations, etc.
An important object associated to an unfolding is its bifurcation set. This set lives in the parameter space of the unfolding, and gives all parameter values for which the resulting function has degenerate singularities.

