
Uniform algebra
Encyclopedia
A uniform algebra A on a compact
Hausdorff
topological space
X is a closed (with respect to the uniform norm) subalgebra
of the C*-algebra C(X) (the continuous complex valued functions on X) with the following properties:
As a closed subalgebra of the commutative Banach algebra
C(X) a uniform algebra is itself a unital commutative Banach algebra (when equipped with the uniform norm). Hence, it is, (by definition) a Banach function algebra
.
A uniform algebra A on X is said to be natural if the maximal ideal
s of A precisely are the ideals of functions vanishing at a point x in X.
of functions vanishing at a point x in X.
such that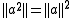 for all a in A, then there is a compact
for all a in A, then there is a compact
Hausdorff
X such that A is isomorphic as a Banach algebra to a uniform algebra on X. This result follows from the spectral radius formula and the Gelfand representation.
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a closed (with respect to the uniform norm) subalgebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of the C*-algebra C(X) (the continuous complex valued functions on X) with the following properties:
- the constant functions are contained in A
- for every x, y
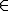 X there is f
X there is f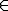 A with f(x)
A with f(x) f(y). This is called separating the points of X.
f(y). This is called separating the points of X.
As a closed subalgebra of the commutative Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
C(X) a uniform algebra is itself a unital commutative Banach algebra (when equipped with the uniform norm). Hence, it is, (by definition) a Banach function algebra
Banach function algebra
In functional analysis a Banach function algebra on a compact Hausdorff space X is unital subalgebra, A of the commutative C*-algebra C of all continuous, complex valued functions from X, together with a norm on A which makes it a Banach algebra.For every x\in X define \varepsilon_x=f\...
.
A uniform algebra A on X is said to be natural if the maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s of A precisely are the ideals
 of functions vanishing at a point x in X.
of functions vanishing at a point x in X.Abstract characterization
If A is a unital commutative Banach algebraBanach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
such that
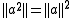 for all a in A, then there is a compact
for all a in A, then there is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
X such that A is isomorphic as a Banach algebra to a uniform algebra on X. This result follows from the spectral radius formula and the Gelfand representation.

