Uniqueness theorem
Encyclopedia
The uniqueness theorem for Poisson's equation
states that the equation has a unique gradient
of the solution for a large class of boundary conditions. In the case of electrostatics
, this means that if an electric field
satisfying the boundary conditions is found, then it is the complete electric field.
, the general expression for Poisson's equation
in electrostatics
is
Here
is the electric potential
and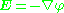
is the electric field
.
The uniqueness of the gradient of the solution (the uniqueness of the electric field) can be proven for a large class of boundary conditions in the following way.
Suppose that there are two solutions
and 
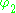. One can then define 
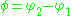which is the difference of the two solutions. Given that both 
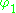and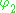 
satisfy Poisson's Equation
,
must satisfy
Using the identity
And noticing that the second term is zero one can rewrite this as
Taking the volume integral over all space specified by the boundary conditions gives
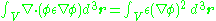
Applying the divergence theorem
, the expression can be rewritten as
Where
are boundary surfaces specified by boundary conditions.
Since
and 
, then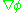 
must be zero everywhere (and so 
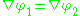) when the surface integral vanishes.
This means that the gradient of the solution is unique when
The boundary conditions for which the above is true are:
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
states that the equation has a unique gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the solution for a large class of boundary conditions. In the case of electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, this means that if an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
satisfying the boundary conditions is found, then it is the complete electric field.
Proof
In Gaussian unitsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, the general expression for Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
is
Here
is the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and
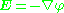is the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
.
The uniqueness of the gradient of the solution (the uniqueness of the electric field) can be proven for a large class of boundary conditions in the following way.
Suppose that there are two solutions
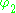and . One can then define 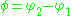which is the difference of the two solutions. Given that both 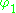and 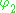satisfy Poisson's EquationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
,
must satisfyUsing the identity
And noticing that the second term is zero one can rewrite this as
Taking the volume integral over all space specified by the boundary conditions gives
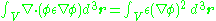
Applying the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, the expression can be rewritten as
Where
are boundary surfaces specified by boundary conditions.Since
and , then 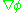must be zero everywhere (and so 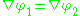) when the surface integral vanishes.This means that the gradient of the solution is unique when
The boundary conditions for which the above is true are:
- Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
:
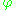is well defined at all of the boundary surfaces. As such 
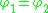so at the boundary 
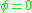and correspondingly the surface integral vanishes. - Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
:
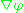is well defined at all of the boundary surfaces. As such 
so at the boundary 
and correspondingly the surface integral vanishes. - Modified Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
(where boundaries are specified as conductors with known charges):
is also well defined by applying locally Gauss's LawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
. As such, the surface integral also vanishes. - Mixed boundary conditions (a combination of Dirichlet, Neumann, and modified Neumann boundary conditions): the uniqueness theorem will still hold.
See also
- Poisson's equationPoisson's equationIn mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
- Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
- Coulomb's lawCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
- Method of imagesMethod of imagesSee also Method of image charges for applications in electrostatics and magnetostaticsMethod of images is a mathematical tool for solving differential equations in which the domain of the sought function is extended by the addition of its mirror image with respect to a symmetry hyperplane, with...
- Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
- Uniqueness theoremUniqueness theoremThe uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
- Spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...