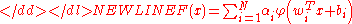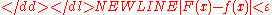In the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 theory of neural networks

Neural Networks

Neural Networks is the official journal of the three oldest societies dedicated to research in neural networks: International Neural Network Society, European Neural Network Society and Japanese Neural Network Society, published by Elsevier...

, the universal approximation theorem states that the standard multilayer

Multilayer perceptron

A multilayer perceptron is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a...

 feed-forward network with a single hidden layer that contains finite number of hidden neuron

Neuron

A neuron is an electrically excitable cell that processes and transmits information by electrical and chemical signaling. Chemical signaling occurs via synapses, specialized connections with other cells. Neurons connect to each other to form networks. Neurons are the core components of the nervous...

s, and with arbitrary activation function are universal approximators on a compact subset of Rⁿ

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

.

The theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

 was proved by George Cybenko in 1989 for a sigmoid

Sigmoid function

Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...

 activation function, thus it is also called the Cybenko theorem.

Kurt Hornik (1991) showed that it is not the specific choice of the activation function, but rather the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators. The output units are always assumed to be linear. For notational convenience we shall explicitly formulate our results only for the case where there is only one output unit. (The general case can easily be deduced from the simple case.)

The theorem in mathematical terms:

Formal statement

Let φ(·) be a nonconstant, bounded, and monotonically

Monotonic function

In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....

-increasing continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

function. Let I_m denote the m-dimensional unit hypercube [0,1]^m. The space of continuous functions on I_m is denoted by C(I_m). Then, given any function f ∈ C(I_m) and є > 0, there exist an integer N and sets of real constants α_i, b_i ∈ R, w_i ∈ R^m, where i = 1, ..., N such that we may define:

as an approximate realization of the function f; that is,

for all x ∈ I_m.