Universal variable formulation
Encyclopedia
In orbital mechanics, the universal variable formulation is a method used to solve the two-body
Kepler problem
. It is a generalized form of Kepler's Equation
s, extending them to apply not only to elliptic orbits, but also parabolic and hyperbolic orbits. It thus is applicable to many situations in the solar system
, where orbits of widely varying eccentricities
are present.
and a time t0, find the position of the body at any other given time t.
For elliptical orbits with a reasonably small eccentricity
, solving Kepler's Equation
by methods like Newton's method
gives adequate results. However, as the orbit becomes more and more eccentric, the numerical iteration may start to converge
slowly or not at all. Furthermore, Kepler's equation cannot be applied to parabolic and hyperbolic orbits, since it specifically is tailored to elliptic orbits.
E, and having a single equation that can be solved regardless of the eccentricity of the orbit. The new variable s is defined by the following differential equation
:
where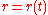
is the time-dependent distance to the center of attraction. The fundamental equation 
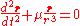is regularized
by applying this change of variables to yield: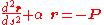
where P is a constant vector and
is defined by
The equation is the same as the equation for the harmonic oscillator
, a well-known equation in both physics
and mathematics
. Taking the derivative again, we get a third-degree differential equation: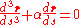
The family of solutions to this differential equation are written symbolically as the functions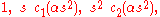
where the functions 
, called Stumpff functions, are generalizations of sine and cosine functions. Applying this results in: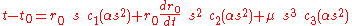
which is the universal variable formulation of Kepler's Equation. This equation can now be solved numerically using a root-finding algorithm
such as Newton's method
or Laguerre's method
for a given time
to yield 
, which in turn is used to compute the f and g functions: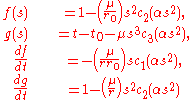
The values of the f and g functions determine the position of the body at the time
:
where
is the position at time 
, and 
and 
are the position and velocity, respectively, at arbitrary initial time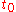 
.
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
. It is a generalized form of Kepler's Equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
s, extending them to apply not only to elliptic orbits, but also parabolic and hyperbolic orbits. It thus is applicable to many situations in the solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
, where orbits of widely varying eccentricities
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
are present.
Introduction
A common problem in orbital mechanics is the following: given a body in an orbitOrbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
and a time t0, find the position of the body at any other given time t.
For elliptical orbits with a reasonably small eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
, solving Kepler's Equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
by methods like Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
gives adequate results. However, as the orbit becomes more and more eccentric, the numerical iteration may start to converge
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
slowly or not at all. Furthermore, Kepler's equation cannot be applied to parabolic and hyperbolic orbits, since it specifically is tailored to elliptic orbits.
Derivation
Although equations similar to Kepler's equation can be derived for parabolic and hyperbolic orbits, it is more convenient to introduce a new independent variable to take the place of the eccentric anomalyEccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
E, and having a single equation that can be solved regardless of the eccentricity of the orbit. The new variable s is defined by the following differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
:
where
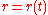is the time-dependent distance to the center of attraction. The fundamental equation 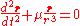is regularizedRegularization
Regularization may refer to:* Regularization ** Regularization * Regularization * Regularization * Regularization...
by applying this change of variables to yield:
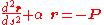
where P is a constant vector and
is defined byThe equation is the same as the equation for the harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
, a well-known equation in both physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Taking the derivative again, we get a third-degree differential equation:
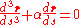
The family of solutions to this differential equation are written symbolically as the functions
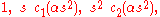where the functions , called Stumpff functions, are generalizations of sine and cosine functions. Applying this results in: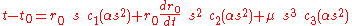which is the universal variable formulation of Kepler's Equation. This equation can now be solved numerically using a root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
such as Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
or Laguerre's method
Laguerre's method
In numerical analysis, Laguerre's method is a root-finding algorithm tailored to polynomials. In other words, Laguerre's method can be used to solve numerically the equation\ p = 0 for a given polynomial p...
for a given time
to yield , which in turn is used to compute the f and g functions: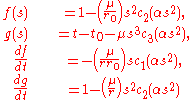The values of the f and g functions determine the position of the body at the time
:where
is the position at time , and and are the position and velocity, respectively, at arbitrary initial time 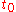.