Upper topology
Encyclopedia
In mathematics
, the upper topology on a partially ordered set
X is the coarsest topology in which the closure of a singleton
is the order section 
for each 
. If 
is a partial order, the upper topology is the least order consistent topology in which the open set
s are the up-sets. The lower topology induced by the preorder is defined similarly in terms of the down-sets. The preoder inducing the upper topology is its specialization preorder, but the specialization preorder of the lower topology is opposite to the inducing preorder.
The real upper topology is most naturally defined on the upper-extended real line
by the system 
of open sets. Similarly, the real lower topology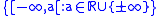 
is naturally defined on the lower real line 
. A real function on a topological space is upper semi-continuous if and only if it is lower-continuous, i.e. is continuous
with respect to the lower topology on the lower-extended line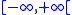
. Similarly, a function into the upper real line is lower semi-continuous if and only if it is upper-continuous, i.e. is continuous
with respect to the upper topology on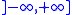
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the upper topology on a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
X is the coarsest topology in which the closure of a singleton
is the order section for each . If is a partial order, the upper topology is the least order consistent topology in which the open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s are the up-sets. The lower topology induced by the preorder is defined similarly in terms of the down-sets. The preoder inducing the upper topology is its specialization preorder, but the specialization preorder of the lower topology is opposite to the inducing preorder.
The real upper topology is most naturally defined on the upper-extended real line
by the system of open sets. Similarly, the real lower topology 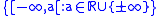is naturally defined on the lower real line . A real function on a topological space is upper semi-continuous if and only if it is lower-continuous, i.e. is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with respect to the lower topology on the lower-extended line
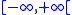. Similarly, a function into the upper real line is lower semi-continuous if and only if it is upper-continuous, i.e. is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with respect to the upper topology on
.
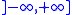