In mathematics, for positive integers k and s, a vectorial addition chain is a sequence V of k-dimensional vectors of nonnegative integers v_i for −k + 1 ≤ i ≤ s together with a sequence w,
such that

v_-k+1 = [1,0,0,,...0,0]

v_-k+2 = [0,1,0,,...0,0]

.

.

v₀ = [0,0,0,,...0,1]

v_i =v_j+v_r for all 1≤i≤s with -k+1≤j,r≤i-1

v_s = [n₀,...,n_k-1]

w = (w₁,...w_s), w_i=(j,r).

For example, a vectorial addition chain for [22,18,3] is

V=([1,0,0],[0,1,0],[0,0,1],[1,1,0],[2,2,0],[4,4,0],[5,4,0],[10,8,0],[11,9,0],[11,9,1],[22,18,2],[22,18,3])

w=((-2,-1),(1,1),(2,2),(-2,3),(4,4),(1,5),(0,6),(7,7),(0,8))

Vectorial addition chains are well suited to perform multi-exponentiation

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

.

Input: Elements x₀,...,x_k-1 of an abelian group

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

 G and a vectorial addition chain of dimension k computing [n₀,...,n_k-1]

Output:The element x₀^n₀...x_k-1^n_r-1

1. for i =-k+1 to 0 do y_i 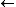x_i+k-1
2. for i = 1 to s do y_i y_j×y_r
3. return y_s

Addition sequence

An addition sequence for the set of integer S ={n₀, ...,n_r-1} is an addition chain

Addition chain

In mathematics, an addition chain for computing a positive integer n can be given by a sequence of natural numbers v and a sequence of index pairs w such that each term in v is the sum of two previous terms, the indices of those terms being specified by w:Often only v is given since it is easy to...

 v that contains every element of S.

For example, an addition sequence computing

{47,117,343,499}

is.

It's possible to find addition sequence from vectorial addition chains and vice versa, so they are in a sense dual.

See also

• Addition chain
  Addition chain
  In mathematics, an addition chain for computing a positive integer n can be given by a sequence of natural numbers v and a sequence of index pairs w such that each term in v is the sum of two previous terms, the indices of those terms being specified by w:Often only v is given since it is easy to...
  
  
• Addition-chain exponentiation
  Addition-chain exponentiation
  In mathematics and computer science, optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications. It works by creating a shortest addition chain that generates the desired exponent. Each exponentiation in the chain...
  
  
• Exponentiation by squaring
  Exponentiation by squaring
  Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
  
  
• Non-adjacent form
  Non-adjacent form
  The non-adjacent form of a number is a unique signed-digit representation. Like the name suggests, non-zero values cannot be adjacent. For example:2 = 4 + 2 + 1 = 72 = 8 − 2 + 1 = 72 = 8 − 4 + 2 + 1 = 72 = 8 − 1 = 7...