Vedic square
Encyclopedia
In ancient Indian mathematics
, a Vedic
square is a variation on a typical 9 × 9 multiplication table
. The entry in each cell is the digital root
of the product of the column and row headings i.e. the remainder
when the product of the row and column headings is divided by 9 (with remainder 0 represented by 9).
Numerous geometric patterns and symmetries can be observed in a Vedic square some of which can be found in traditional Islamic art
(Pritchard, 2003).
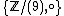where 
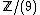is the set of positive integers partitioned by the residue classes modulo nine. Also, the operator 
means the abstract "multiplication" between the elements of this monoid. If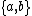 
are elements of 
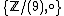then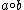 
can be seen as,
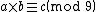where we take the element 9 as the representative of the residue class of 0 rather than the traditional choice of 0.
This does not form a group
since not every non-zero element has a corresponding inverse element, for example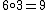
but there is no 
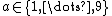such that 
.
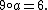If we consider the subset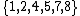
, however, this does form a group. It forms a cyclic group with 2 as one choice of generator. In fact, this is just the group of multiplicative units in the ring 
.
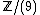Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, a Vedic
Vedic
Vedic may refer to:* the Vedas, the oldest preserved Indic texts** Vedic Sanskrit, the language of these texts** Vedic period, during which these texts were produced** Vedic pantheon of gods mentioned in Vedas/vedic period...
square is a variation on a typical 9 × 9 multiplication table
Multiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
. The entry in each cell is the digital root
Digital root
The digital root of a number is the value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum...
of the product of the column and row headings i.e. the remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
when the product of the row and column headings is divided by 9 (with remainder 0 represented by 9).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 | 9 |
| 3 | 3 | 6 | 9 | 3 | 6 | 9 | 3 | 6 | 9 |
| 4 | 4 | 8 | 3 | 7 | 2 | 6 | 1 | 5 | 9 |
| 5 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 |
| 6 | 6 | 3 | 9 | 6 | 3 | 9 | 6 | 3 | 9 |
| 7 | 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 | 9 |
| 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
Numerous geometric patterns and symmetries can be observed in a Vedic square some of which can be found in traditional Islamic art
Islamic art
Islamic art encompasses the visual arts produced from the 7th century onwards by people who lived within the territory that was inhabited by or ruled by culturally Islamic populations...
(Pritchard, 2003).
Algebraic Properties
This table can be viewed as the multiplication table of the monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
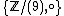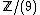where is the set of positive integers partitioned by the residue classes modulo nine. Also, the operator means the abstract "multiplication" between the elements of this monoid. If 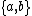are elements of 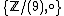then 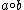can be seen as, 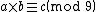where we take the element 9 as the representative of the residue class of 0 rather than the traditional choice of 0.This does not form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
since not every non-zero element has a corresponding inverse element, for example
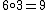but there is no 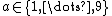such that 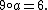.If we consider the subset
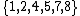, however, this does form a group. It forms a cyclic group with 2 as one choice of generator. In fact, this is just the group of multiplicative units in the ring .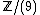