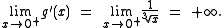In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a vertical tangent is tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 line that is vertical

Vertical direction

In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...

. Because a vertical line has infinite slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

, a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 whose graph

Graph of a function

In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...

 has a vertical tangent is not differentiable at the point of tangency.

Limit definition

A function ƒ has a vertical tangent at x = a if the difference quotient

Difference quotient

The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...

 used to define the derivative has infinite limit:


The first case corresponds to an upward-sloping vertical tangent, and the second case to a downward-sloping vertical tangent. Informally speaking, the graph of ƒ has a vertical tangent at x = a if the derivative of ƒ at a is either positive or negative infinity.

For a continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

, it is often possible to detect a vertical tangent by taking the limit of the derivative. If


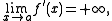
then ƒ must have an upward-sloping vertical tangent at x = a. Similarly, if


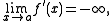
then ƒ must have a downward-sloping vertical tangent at x = a. In these situations, the vertical tangent to ƒ appears as a vertical asymptote

Asymptote

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...

 on the graph of the derivative.

Vertical cusps

Closely related to vertical tangents are vertical cusps

Cusp (singularity)

In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....

. This occurs when the one-sided derivatives are both infinite, but one is positive and the other is negative. For example, if


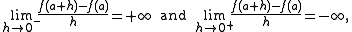
then the graph of ƒ will have a vertical cusp that slopes up on the left side and down on the right side.

As with vertical tangents, vertical cusps can sometimes be detected for a continuous function by examining the limit of the derivative. For example, if
then the graph of ƒ will have a vertical cusp that slopes down on the left side and up on the right side. This corresponds to a vertical asymptote on the graph of the derivative that goes to 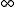on the left and 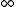on the right.

Example

The function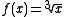
has a vertical tangent at x = 0, since it is continuous and
Similarly, the function
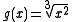
has a vertical cusp at x = 0, since it is continuous,
and