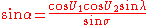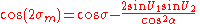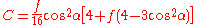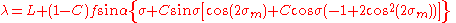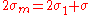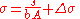Vincenty's formulae
Encyclopedia
Vincenty's formulae are two related iterative method
s used in geodesy
to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty
(1975a) They are based on the assumption that the figure of the Earth
is an oblate spheroid, and hence are more accurate than methods such as great-circle distance
which assume a spherical Earth.
The first (direct) method computes the location of a point which is a given distance and azimuth (direction) from another point. The second (inverse) method computes the geographical distance
and azimuth between two given points. They have been widely used in geodesy because they are accurate to within 0.5 mm (0.020″) on the Earth ellipsoid
.
inverse geodesic problem in a form that minimized the program length
(see the first sentence of his paper). His unpublished report (1975b)
mentions the use of a Wang
720 desk calculator which had only a few
kilobytes of memory. To obtain good accuracy for long lines, the
solution uses the classical solution of Legendre (1806), Bessel (1825),
and Helmert (1880) based on the auxiliary sphere. (Vincenty relied on
formulation of this method given by Rainsford, 1955.) Legendre showed
that an ellipsoidal geodesic can be exactly mapped to a great circle on
the auxiliary sphere by mapping the geographic latitude to reduced
latitude and setting the azimuth of the great circle equal to that of
the geodesic. The longitude on the ellipsoid and the distance along the
geodesic are then given in terms of the longitude on the sphere and the
arc length along the great circle by simple integrals. Bessel and
Helmert gave rapidly converging series for these integrals which allow
the geodesic to be computed with arbitrary accuracy.
In order to minimize the program size, Vincenty took these series,
re-expanded them using the first term of each series as the small
parameter, and truncated them to order ƒ3. This resulted in
compact expressions for the longitude and distance integrals.
The expressions were put in Horner
(or nested) form, since this
allows polynomials to be evaluated using only a single temporary
register. Finally, simple iterative techniques were used
to solve the implicit equations in the direct and inverse methods; even
though these are slow (and in the case of the inverse method it sometimes does
not converge), they result in the least increase in code size.
Calculate U1, U2 and L, and set initial value of λ = L. Then iteratively evaluate the following equations until λ converges:
When λ has converged to the desired degree of accuracy (10−12 corresponds to approximately 0.06mm), evaluate the following:
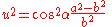
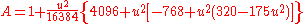
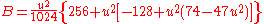
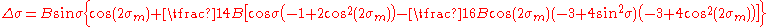
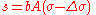
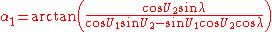
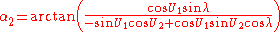
Between two nearly antipodal points, the iterative formula may fail to converge; this will occur when the first guess at λ as computed by the equation above is greater than π in absolute value.
and initial azimuth, α1, and a distance, s, along
the geodesic the Vincenty direct method finds the end point
(φ2, L2) and azimuth,
α2.
Start by calculating the following:
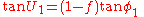

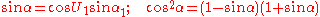
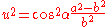
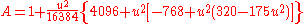
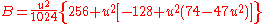
Then, using an initial value , iterate the following equations until
, iterate the following equations until
there is no significant change in σ:
Once σ is obtained to sufficient accuracy evaluate:

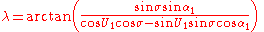
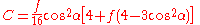
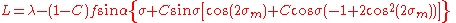

If the initial point is at the North or South pole then the first equation is indeterminate.
If the initial azimuth is due East or West then the second equation is indeterminate.
If a double valued atan2 type function is used then these values are usually handled correctly.
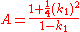
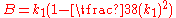
where
for nearly antipodal points. An example of slow convergence is
(φ1, L1) = (0°, 0°) and
(φ2, L2) = (0.5°, 179.5°) for the WGS84
ellipsoid. This requires about 130 iterations to give a result accurate
to 1 mm. Depending on how the inverse method is implemented, the
algorithm might return the correct result (19936288.579 m), an incorrect
result, or an error indicator. An example of an incorrect result is
provided by the NGS online utility which returns a distance which is about 5 km too long.
Vincenty suggested a method of accelerating the convergence in such cases
(Rapp, 1973).
An example of a failure of the inverse method to converge is
(φ1, L1) = (0°, 0°) and
(φ2, L2) = (0.5°, 179.7°) for the WGS84
ellipsoid. In an
unpublished report, Vincenty (1975b) gave an alternative iterative
scheme to handle such cases. This converges to the correct result
19944127.421 m after about 60 iterations;
however, in other cases many thousands of iterations are required.
Newton's method has been successfully used to give rapid convergence for
all pairs input points (Karney, 2011).
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s used in geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty
Thaddeus Vincenty
Thaddeus Vincenty was a Polish American geodesist who worked with the U.S...
(1975a) They are based on the assumption that the figure of the Earth
Figure of the Earth
The expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
is an oblate spheroid, and hence are more accurate than methods such as great-circle distance
Great-circle distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
which assume a spherical Earth.
The first (direct) method computes the location of a point which is a given distance and azimuth (direction) from another point. The second (inverse) method computes the geographical distance
Geographical distance
Geographical distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude.-An abstraction:...
and azimuth between two given points. They have been widely used in geodesy because they are accurate to within 0.5 mm (0.020″) on the Earth ellipsoid
Earth ellipsoid
An Earth ellipsoid is a mathematical figure approximating the shape of the Earth, used as a reference frame for computations in geodesy, astronomy and the geosciences...
.
Background
Vincenty's goal was to express existing algorithms for the direct andinverse geodesic problem in a form that minimized the program length
(see the first sentence of his paper). His unpublished report (1975b)
mentions the use of a Wang
720 desk calculator which had only a few
kilobytes of memory. To obtain good accuracy for long lines, the
solution uses the classical solution of Legendre (1806), Bessel (1825),
and Helmert (1880) based on the auxiliary sphere. (Vincenty relied on
formulation of this method given by Rainsford, 1955.) Legendre showed
that an ellipsoidal geodesic can be exactly mapped to a great circle on
the auxiliary sphere by mapping the geographic latitude to reduced
latitude and setting the azimuth of the great circle equal to that of
the geodesic. The longitude on the ellipsoid and the distance along the
geodesic are then given in terms of the longitude on the sphere and the
arc length along the great circle by simple integrals. Bessel and
Helmert gave rapidly converging series for these integrals which allow
the geodesic to be computed with arbitrary accuracy.
In order to minimize the program size, Vincenty took these series,
re-expanded them using the first term of each series as the small
parameter, and truncated them to order ƒ3. This resulted in
compact expressions for the longitude and distance integrals.
The expressions were put in Horner
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
(or nested) form, since this
allows polynomials to be evaluated using only a single temporary
register. Finally, simple iterative techniques were used
to solve the implicit equations in the direct and inverse methods; even
though these are slow (and in the case of the inverse method it sometimes does
not converge), they result in the least increase in code size.
Notation
Define the following notation:| a | length of major axis of the ellipsoid (radius at equator); | (6378137.0 metres in WGS-84) |
| ƒ | flattening Flattening The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator... of the ellipsoid; |
(1/298.257223563 in WGS-84) |
| b = (1 - ƒ) a | length of minor axis of the ellipsoid (radius at the poles); | |
| φ1, φ2 | latitude Latitude In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a... of the points; |
|
| U1 = arctan[(1 − ƒ) tan φ1], U2 = arctan[(1 − ƒ) tan φ2] |
reduced latitude (latitude on the auxiliary sphere) | |
| L = L2 - L1 | difference in longitude Longitude Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda .... of two points; |
|
| λ1, λ2 | longitude of the points on the auxiliary sphere; | |
| α1, α2 | forward azimuths at the points; | |
| α | azimuth at the equator; | |
| s | ellipsoidal distance between the two points; | |
| σ | arc length between points on the auxiliary spheree; |
Inverse method
Given the coordinates of the two points (φ1, L1) and (φ2, L2), the inverse method finds the azimuths α1, α2 and the ellipsoidal distance s.Calculate U1, U2 and L, and set initial value of λ = L. Then iteratively evaluate the following equations until λ converges:
When λ has converged to the desired degree of accuracy (10−12 corresponds to approximately 0.06mm), evaluate the following:
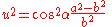
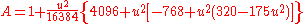
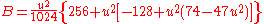
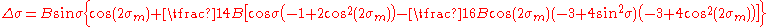
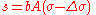
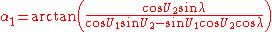
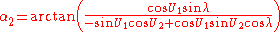
Between two nearly antipodal points, the iterative formula may fail to converge; this will occur when the first guess at λ as computed by the equation above is greater than π in absolute value.
Direct Method
Given an initial point (φ1, L1)and initial azimuth, α1, and a distance, s, along
the geodesic the Vincenty direct method finds the end point
(φ2, L2) and azimuth,
α2.
Start by calculating the following:
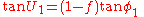

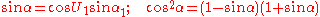
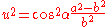
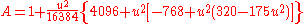
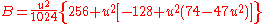
Then, using an initial value
 , iterate the following equations until
, iterate the following equations untilthere is no significant change in σ:
Once σ is obtained to sufficient accuracy evaluate:

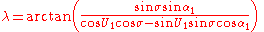
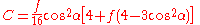
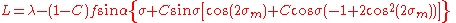

If the initial point is at the North or South pole then the first equation is indeterminate.
If the initial azimuth is due East or West then the second equation is indeterminate.
If a double valued atan2 type function is used then these values are usually handled correctly.
Vincenty's modification
In his letter to Survey Review in 1976, Vincenty suggested replacing his series expressions for A and B with simpler formulas using Helmert's expansion parameter k1: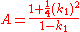
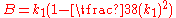
where

Nearly antipodal points
As noted above, the inverse method fails to converge or converges slowlyfor nearly antipodal points. An example of slow convergence is
(φ1, L1) = (0°, 0°) and
(φ2, L2) = (0.5°, 179.5°) for the WGS84
ellipsoid. This requires about 130 iterations to give a result accurate
to 1 mm. Depending on how the inverse method is implemented, the
algorithm might return the correct result (19936288.579 m), an incorrect
result, or an error indicator. An example of an incorrect result is
provided by the NGS online utility which returns a distance which is about 5 km too long.
Vincenty suggested a method of accelerating the convergence in such cases
(Rapp, 1973).
An example of a failure of the inverse method to converge is
(φ1, L1) = (0°, 0°) and
(φ2, L2) = (0.5°, 179.7°) for the WGS84
ellipsoid. In an
unpublished report, Vincenty (1975b) gave an alternative iterative
scheme to handle such cases. This converges to the correct result
19944127.421 m after about 60 iterations;
however, in other cases many thousands of iterations are required.
Newton's method has been successfully used to give rapid convergence for
all pairs input points (Karney, 2011).
See also
- Geographical distanceGeographical distanceGeographical distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude.-An abstraction:...
- Great-circle distanceGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
- Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
- Thaddeus VincentyThaddeus VincentyThaddeus Vincenty was a Polish American geodesist who worked with the U.S...
- GeodesyGeodesyGeodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
External links
- Online calculators from Geoscience AustraliaGeoscience AustraliaGeoscience Australia is an agency of the Australian federal government. It carries out geoscientific research.On a user pays basis it produces geospatial products such as topographic maps and satellite imagery.-History:...
:- Vincenty Direct (destination point)
- Vincenty Inverse (distance between points)
- Calculators from the U.S. National Geodetic SurveyU.S. National Geodetic SurveyNational Geodetic Survey, formerly called the U.S. Coast and Geodetic Survey , is a United States federal agency that defines and manages a national coordinate system, providing the foundation for transportation and communication; mapping and charting; and a large number of applications of science...
:- Online and downloadable PC-executable calculation utilities, including forward (direct) and inverse problems, in both two and three dimensions (accessed 2011-08-01).
- Online calculators with JavaScript source code by Chris Veness (Creative Commons Attribution license):
- Vincenty Direct (destination point)
- Vincenty Inverse (distance between points)
- GeographicLib provides a utility Geod (with MIT/X11 licensed source code) for solving direct and inverse geodesic problems. Compared to Vincenty, this is about 1000 times more accurate (error = 15 nm) and the inverse solution is complete. Here is an online version of Geod.