In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, especially in the area of abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

 which studies infinite group

Infinite group

In group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....

s, the adverb virtually is used to modify a property so that it need only hold for a subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

 of finite index. Given a property P, the group G is said to be virtually P if there is a finite index

Index of a subgroup

In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...

 subgroup H≤G such that H has property P.

Common uses for this would be when P is abelian

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

, nilpotent

Nilpotent group

In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...

, solvable

Solvable group

In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...

 or free

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

. For example, virtually solvable groups are one of the two alternatives in the Tits alternative

Tits alternative

In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about the structure of finitely generated linear groups. It states that every such group is either virtually solvable In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about...

, while Gromov's theorem

Gromov's theorem on groups of polynomial growth

In geometric group theory, Gromov's theorem on groups of polynomial growth, named for Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index....

 states that the finitely generated groups with polynomial growth

Growth rate (group theory)

In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...

 are precisely the finitely generated virtually nilpotent groups.

This terminology is also used when P is just another group. That is, if G and H are groups then G is virtually H if G has a subgroup K of finite index in G such that K is isomorphic

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

 to H.

A consequence of this is that a finite group is virtually trivial.

Virtually abelian

The following groups are virtually abelian.

• Any abelian group.
• Any semidirect product
  Semidirect product
  In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
  
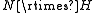    where N is abelian and H is finite. (For example, any generalized dihedral group
  Generalized dihedral group
  In mathematics, the generalized dihedral groups are a family of groups with algebraic structures similar to that of the dihedral groups. They include the finite dihedral groups, the infinite dihedral group, and the orthogonal group O.-Definition:...
  
  .)
• Any semidirect product 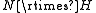where N is finite and H is abelian.
• Any finite group (since the trivial subgroup is abelian).

Virtually nilpotent

• Any group that is virtually abelian.
• Any nilpotent group.
• Any semidirect product where N is nilpotent and H is finite.
• Any semidirect product 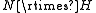where N is finite and H is nilpotent.

Virtually free

• Any free group
  Free group
  In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
  
  .
• Any virtually cyclic group.
• Any semidirect product 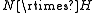where N is free and H is finite.
• Any semidirect product 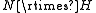where N is finite and H is free.
• Any free product
  Free product
  In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
  
   H * K, where H and K are both finite. (For example, the modular group
  Modular group
  In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
  
   PSL(2,Z).)

Others

The free group F₂ on 2 generators is virtually F_n for any n ≥ 2 as a consequence of the Nielsen–Schreier theorem

Nielsen–Schreier theorem

In group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...

and the Schreier index formula.

External links

• Schreier index formula at PlanetMath.