
Von Kármán constant
Encyclopedia
In fluid dynamics
, the Von Kármán constant (or Kármán constant), named for Theodore von Kármán
, is a dimensionless constant describing the logarithm
ic velocity profile of a turbulent fluid flow near a boundary with a no-slip condition
. The equation for such boundary layer
flow profiles is:
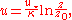
where u is the mean flow velocity
at height z above the boundary. The roughness height (also known as roughness length
) z0 is where appears to go to zero. Further κ is the von Kármán constant (typically the value 0.41 is used), and
appears to go to zero. Further κ is the von Kármán constant (typically the value 0.41 is used), and 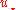 is the friction velocity which depends on the shear stress
is the friction velocity which depends on the shear stress
τw at the boundary of the flow:
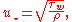
with ρ the fluid density
.
The Kármán constant is often used in turbulence modeling, for instance in boundary-layer meteorology
to calculate flux
es of momentum
, heat and moisture from the atmosphere to the land surface.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Von Kármán constant (or Kármán constant), named for Theodore von Kármán
Theodore von Karman
Theodore von Kármán was a Hungarian-American mathematician, aerospace engineer and physicist who was active primarily in the fields of aeronautics and astronautics. He is responsible for many key advances in aerodynamics, notably his work on supersonic and hypersonic airflow characterization...
, is a dimensionless constant describing the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic velocity profile of a turbulent fluid flow near a boundary with a no-slip condition
No-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
. The equation for such boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
flow profiles is:
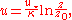
where u is the mean flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
at height z above the boundary. The roughness height (also known as roughness length
Roughness Length
Roughness length is a parameter of some vertical wind profile equations that model the horizontal mean wind speed near the ground; in the log wind profile, it is equivalent to the height at which the wind speed is zero. It is so named because it is typically related to the height of terrain...
) z0 is where
 appears to go to zero. Further κ is the von Kármán constant (typically the value 0.41 is used), and
appears to go to zero. Further κ is the von Kármán constant (typically the value 0.41 is used), and 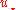 is the friction velocity which depends on the shear stress
is the friction velocity which depends on the shear stressShear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
τw at the boundary of the flow:
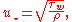
with ρ the fluid density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
.
The Kármán constant is often used in turbulence modeling, for instance in boundary-layer meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
to calculate flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, heat and moisture from the atmosphere to the land surface.
External links
- http://www.ccsm.ucar.edu/models/ccsm3.0/cpl6/users_guide/node21.html a list of physical constants used in the NCAR Community Climate System Model

