Von Mises stress
Encyclopedia
The von Mises yield criterion suggests that the yielding
of materials begins when the second deviatoric stress invariant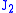 reaches a critical value
reaches a critical value  . For this reason, it is sometimes called the
. For this reason, it is sometimes called the 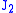 -plasticity or
-plasticity or 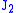 flow theory. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response is assumed to be elastic
flow theory. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response is assumed to be elastic
.
In materials science
and engineering
the von Mises yield criterion can be also formulated in terms of the von Mises stress or equivalent tensile stress,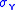 , a scalar stress value that can be computed from the stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength,
, a scalar stress value that can be computed from the stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength, 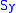 . The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.
. The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.
Because the von Mises yield criterion
is independent of the first stress invariant,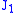 , it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensor
, it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensor
.
Although formulated by Maxwell
in 1865, it is generally attributed to Richard Edler von Mises (1913). Tytus Maksymilian Huber (1904), in a paper in Polish, anticipated to some extent this criterion. This criterion is also referred to as the Maxwell
–Huber
–Hencky
–von Mises theory.
 Mathematically the von Mises yield
Mathematically the von Mises yield
criterion is expressed as:
where is the yield stress of the material in pure shear. As shown later in this article, at the onset of yielding, the magnitude of the shear yield stress in pure shear is √3 times lower than the tensile yield stress in the case of simple tension. Thus, we have:
is the yield stress of the material in pure shear. As shown later in this article, at the onset of yielding, the magnitude of the shear yield stress in pure shear is √3 times lower than the tensile yield stress in the case of simple tension. Thus, we have: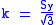
where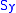 is the yield strength of the material. If we set the von Mises stress equal to the yield strength and combine the above equations, the von Mises yield criterion and expressed as:
is the yield strength of the material. If we set the von Mises stress equal to the yield strength and combine the above equations, the von Mises yield criterion and expressed as: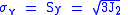
or
Substituting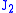 with terms of the stress tensor components
with terms of the stress tensor components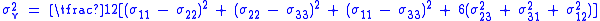
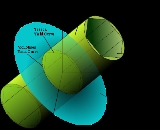
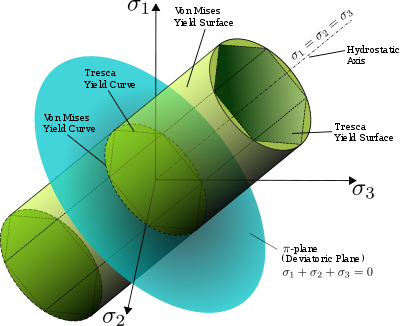
This equation defines the yield surface
as a circular cylinder (See Figure) whose yield curve
, or intersection with the deviatoric plane, is a circle with radius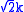 , or
, or 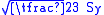 . This implies that the yield condition is independent of hydrostatic stresses.
. This implies that the yield condition is independent of hydrostatic stresses.
 Notes:
Notes:
In the case of uniaxial stress or simple tension,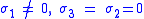 , the von Mises criterion simply reduces to
, the von Mises criterion simply reduces to ,
,
which means the material starts to yield when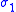 reaches the yield strength of the material
reaches the yield strength of the material 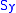 , and is agreement with the definition of tensile (or compressive) yield strength.
, and is agreement with the definition of tensile (or compressive) yield strength.
It is also convenient to define an Equivalent tensile stress or von Mises stress,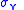 , which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. Thus, we define
, which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. Thus, we define
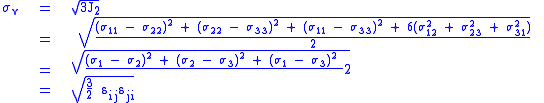
where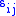 are the components of the stress deviator tensor
are the components of the stress deviator tensor 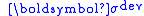 :
:
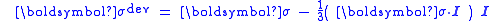 .
.
In this case, yielding occurs when the equivalent stress, , reaches the yield strength of the material in simple tension,
, reaches the yield strength of the material in simple tension,  . As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom, because the stress tensor has six independent components. Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i.e., one degree of freedom, this comparison is straightforward: A larger von Mises value implies that the material is closer to the yield point.
. As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom, because the stress tensor has six independent components. Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i.e., one degree of freedom, this comparison is straightforward: A larger von Mises value implies that the material is closer to the yield point.
In the case of pure shear stress,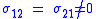 , while all other
, while all other 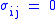 , von Mises criterion becomes:
, von Mises criterion becomes:
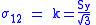 .
.
This means that, at the onset of yielding, the magnitude of the shear stress in pure shear is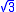 times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is
times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is
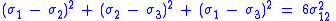
In the case of plane stress, , the von Mises criterion becomes:
, the von Mises criterion becomes:
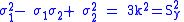
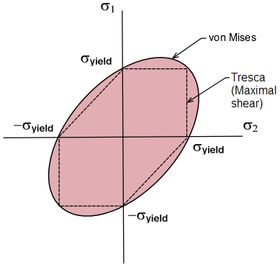
This equation represents an ellipse in the plane , as shown in the Figure above.
, as shown in the Figure above.
(1924) offered a physical interpretation of von Mises criterion suggesting that yielding begins when the elastic energy of distortion reaches a critical value. For this, the von Mises criterion is also known as the maximum distortion strain energy criterion. This comes from the relation between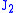 and the elastic strain energy of distortion
and the elastic strain energy of distortion  :
:
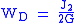 with the elastic shear modulus
with the elastic shear modulus 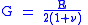 .
.
In 1937 Arpad L. Nadai suggested that yielding begins when the octahedral shear stress reaches a critical value, i.e. the octahedral shear stress of the material at yield in simple tension. In this case, the von Mises yield criterion is also known as the maximum octahedral shear stress criterion in view of the direct proportionality that exist between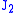 and the octahedral shear stress,
and the octahedral shear stress, 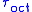 , which by definition is
, which by definition is
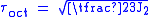
thus we have

's maximum shear stress criterion (dashed line). Observe that Tresca's yield surface is circumscribed by von Mises'. Therefore, it predicts plastic yielding already for stress states that are still elastic according to the von Mises criterion. As a model for plastic material behavior, Tresca's criterion is therefore more conservative.
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
of materials begins when the second deviatoric stress invariant
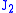 reaches a critical value
reaches a critical value  . For this reason, it is sometimes called the
. For this reason, it is sometimes called the 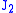 -plasticity or
-plasticity or 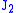 flow theory. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response is assumed to be elastic
flow theory. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response is assumed to be elasticElasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
.
In materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
the von Mises yield criterion can be also formulated in terms of the von Mises stress or equivalent tensile stress,
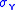 , a scalar stress value that can be computed from the stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength,
, a scalar stress value that can be computed from the stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength, 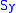 . The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.
. The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.Because the von Mises yield criterion
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
is independent of the first stress invariant,
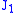 , it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensor
, it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensorHydrostatic stress
In continuum mechanics, a hydrostatic stress is an isotropic stress that is given by the weight of water above a certain point. It is often used interchangeably with "pressure" and is also known as confining stress, particularly in the field geomechanics...
.
Although formulated by Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in 1865, it is generally attributed to Richard Edler von Mises (1913). Tytus Maksymilian Huber (1904), in a paper in Polish, anticipated to some extent this criterion. This criterion is also referred to as the Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
–Huber
Tytus Maksymilian Huber
Tytus Maksymilian Huber was a world renowned Polish mechanical engineer, educator, and scientist. He was a member of the pre-war Polish scientific foundation, Kasa im...
–Hencky
Heinrich Hencky
Heinrich Hencky was a German engineer.Born in Ansbach he studied civil engineering in Munich and received his PhD from the Technische Hochschule Darmstadt. In 1913 Hencky joins a railway company in Kharkiv, Ukraine. At the outbreak of World War I he was interned...
–von Mises theory.
Mathematical formulation

Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
criterion is expressed as:

where
 is the yield stress of the material in pure shear. As shown later in this article, at the onset of yielding, the magnitude of the shear yield stress in pure shear is √3 times lower than the tensile yield stress in the case of simple tension. Thus, we have:
is the yield stress of the material in pure shear. As shown later in this article, at the onset of yielding, the magnitude of the shear yield stress in pure shear is √3 times lower than the tensile yield stress in the case of simple tension. Thus, we have: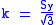
where
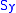 is the yield strength of the material. If we set the von Mises stress equal to the yield strength and combine the above equations, the von Mises yield criterion and expressed as:
is the yield strength of the material. If we set the von Mises stress equal to the yield strength and combine the above equations, the von Mises yield criterion and expressed as: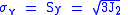
or

Substituting
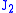 with terms of the stress tensor components
with terms of the stress tensor components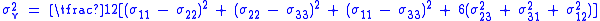
This equation defines the yield surface
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
as a circular cylinder (See Figure) whose yield curve
Yield curve
In finance, the yield curve is the relation between the interest rate and the time to maturity, known as the "term", of the debt for a given borrower in a given currency. For example, the U.S. dollar interest rates paid on U.S...
, or intersection with the deviatoric plane, is a circle with radius
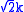 , or
, or 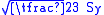 . This implies that the yield condition is independent of hydrostatic stresses.
. This implies that the yield condition is independent of hydrostatic stresses.Reduced von Mises equation for different stress conditions
The above equation can be reduced and reorganized for practical use in different loading scenarios.| Load scenario | Restrictions | Simplified von Mises equation |
|---|---|---|
| General | No restrictions | 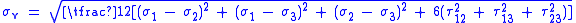 |
| Principal stresses | 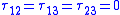 |
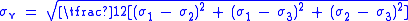 |
| 2D plane | 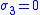 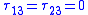 |
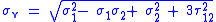 |
| Pure shear | 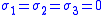  |
 |
| Uniaxial | 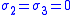 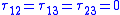 |
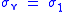 |

- subscripts 1,2,3 can be replaced with x,y,z, or other orthogonal coordinate system
In the case of uniaxial stress or simple tension,
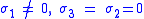 , the von Mises criterion simply reduces to
, the von Mises criterion simply reduces to ,
,which means the material starts to yield when
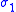 reaches the yield strength of the material
reaches the yield strength of the material 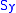 , and is agreement with the definition of tensile (or compressive) yield strength.
, and is agreement with the definition of tensile (or compressive) yield strength.It is also convenient to define an Equivalent tensile stress or von Mises stress,
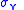 , which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. Thus, we define
, which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. Thus, we define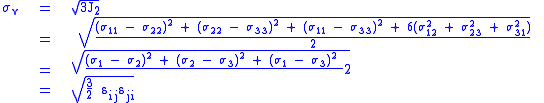
where
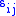 are the components of the stress deviator tensor
are the components of the stress deviator tensor 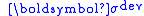 :
: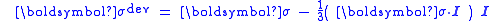 .
.In this case, yielding occurs when the equivalent stress,
 , reaches the yield strength of the material in simple tension,
, reaches the yield strength of the material in simple tension,  . As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom, because the stress tensor has six independent components. Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i.e., one degree of freedom, this comparison is straightforward: A larger von Mises value implies that the material is closer to the yield point.
. As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom, because the stress tensor has six independent components. Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i.e., one degree of freedom, this comparison is straightforward: A larger von Mises value implies that the material is closer to the yield point.In the case of pure shear stress,
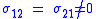 , while all other
, while all other 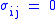 , von Mises criterion becomes:
, von Mises criterion becomes: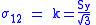 .
.This means that, at the onset of yielding, the magnitude of the shear stress in pure shear is
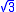 times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is
times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is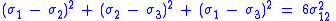
In the case of plane stress,
 , the von Mises criterion becomes:
, the von Mises criterion becomes: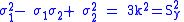
This equation represents an ellipse in the plane
 , as shown in the Figure above.
, as shown in the Figure above.Physical interpretation of the von Mises yield criterion
HenckyHeinrich Hencky
Heinrich Hencky was a German engineer.Born in Ansbach he studied civil engineering in Munich and received his PhD from the Technische Hochschule Darmstadt. In 1913 Hencky joins a railway company in Kharkiv, Ukraine. At the outbreak of World War I he was interned...
(1924) offered a physical interpretation of von Mises criterion suggesting that yielding begins when the elastic energy of distortion reaches a critical value. For this, the von Mises criterion is also known as the maximum distortion strain energy criterion. This comes from the relation between
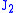 and the elastic strain energy of distortion
and the elastic strain energy of distortion  :
: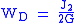 with the elastic shear modulus
with the elastic shear modulus 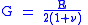 .
.In 1937 Arpad L. Nadai suggested that yielding begins when the octahedral shear stress reaches a critical value, i.e. the octahedral shear stress of the material at yield in simple tension. In this case, the von Mises yield criterion is also known as the maximum octahedral shear stress criterion in view of the direct proportionality that exist between
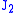 and the octahedral shear stress,
and the octahedral shear stress, 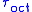 , which by definition is
, which by definition is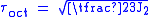
thus we have

Comparison with Tresca yield criterion
Also shown in the figure is TrescaHenri Tresca
Henri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
's maximum shear stress criterion (dashed line). Observe that Tresca's yield surface is circumscribed by von Mises'. Therefore, it predicts plastic yielding already for stress states that are still elastic according to the von Mises criterion. As a model for plastic material behavior, Tresca's criterion is therefore more conservative.
See also
- Yield surfaceYield surfaceA yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
- Henri TrescaHenri TrescaHenri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
- Mohr-Coulomb theoryMohr-Coulomb theoryMohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- StressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- StrainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
- 3-D elasticity

