Mohr-Coulomb theory
Encyclopedia
Mohr–Coulomb theory is a mathematical model
(see yield surface
) describing the response of brittle materials such as concrete
, or rubble piles, to shear stress
as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.
In Geotechnical Engineering
it is used to define shear strength of soils and rocks at different effective stress
es.
In structural engineering
it is used to determine failure load as well as the angle of fracture
of a displacement fracture in concrete and similar materials. Coulomb
's friction
hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. Mohr's circle is used to determine which principal stresses that will produce this combination of shear and normal stress, and the angle of the plane in which this will occur. According to the principle of normality the stress introduced at failure will be perpendicular to the line describing the fracture condition.
It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the angle of friction. This makes the strength of the material determinable by comparing the external mechanical work
introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By conservation of energy
the sum of these must be zero and this will make it possible to calculate the failure load of the construction.
A common improvement of this model is to combine Coulomb's friction hypothesis with Rankine's
principal stress hypothesis to describe a separation fracture.
and Christian Otto Mohr. Coulomb's contribution was a 1776 essay entitled "Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l'architecture"
.
Mohr developed a generalised form of the theory around the end of the 19th century.
As the generalised form affected the interpretation of the criterion, but not the substance of it, some texts continue to refer to the criterion as simply the 'Coulomb criterion'.
where
is the shear strength, 
is the normal stress, 
is the intercept of the failure envelope with the 
axis, and 
is the slope of the failure envelope. The quantity 
is often called the cohesion and the angle 
is called the angle of internal friction . Compression is assumed to be positive in the following discussion. If compression is assumed to be negative then 
should be replaced with 
.
If
, the Mohr–Coulomb criterion reduces to the Tresca criterion. On the other hand, if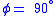 
the Mohr–Coulomb model is equivalent to the Rankine model. Higher values of 
are not allowed.
From Mohr's circle we have
where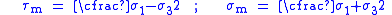
and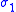
is the maximum principal stress and 
is the minimum principal stress.
Therefore the Mohr–Coulomb criterion may also be expressed as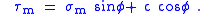
This form of the Mohr–Coulomb criterion is applicable to failure on a plane that is parallel to the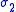
direction.
The Mohr–Coulomb failure surface is a cone with a hexagonal cross section in deviatoric stress space.
The expressions for
and 
can be generalized to three dimensions by developing expressions for the normal stress and the resolved shear stress on a plane of arbitrary orientation with respect to the coordinate axes (basis vectors). If the unit normal to the plane of interest is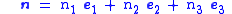
where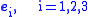
are three orthonormal unit basis vectors, and if the principal stresses 
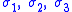are aligned with the basis vectors 
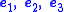, then the expressions for 
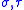are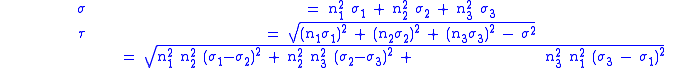
The Mohr–Coulomb failure criterion can then be evaluated using the usual expression
for the six planes of maximum shear stress.
{| class="toccolours collapsible collapsed" width="60%" style="text-align:left"
!Derivation of normal and shear stress on a plane
|-
|Let the unit normal to the plane of interest be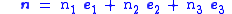
where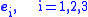
are three orthonormal unit basis vectors. Then the traction vector on the plane is given by
The magnitude of the traction vector is given by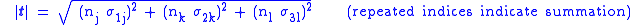
Then the magnitude of the stress normal to the plane is given by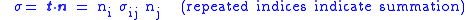
The magnitude of the resolved shear stress on the plane is given by
In terms of components, we have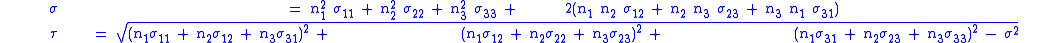
If the principal stresses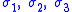
are aligned with the basis vectors 
, then the expressions for 
are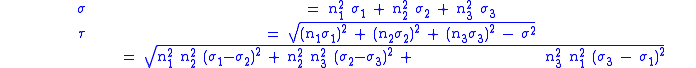
|}
{| border="0"
|-
| valign="bottom"|
|
|
| valign="bottom"|
|-
|}
can be expressed as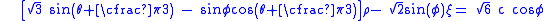
Alternatively, in terms of the invariants
we can write
where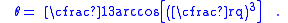
{| class="toccolours collapsible collapsed" width="80%" style="text-align:left"
!Derivation of alternative forms of Mohr–Coulomb yield function
|-
|We can express the yield function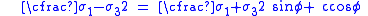
as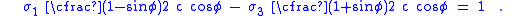
The Haigh–Westergaard invariants are related to the principal stresses by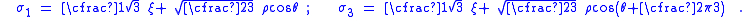
Plugging into the expression for the Mohr–Coulomb yield function gives us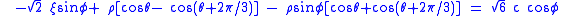
Using trigonometric identities for the sum and difference of cosines and rearrangement gives us the expression of the Mohr–Coulomb yield function in terms of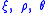
.
We can express the yield function in terms of
by using the relations
and straightforward substitution.
|}
A common approach that is used is to use a non-associated plastic flow potential that is smooth. An example of such a potential is the function
where
is a parameter, 
is the value of 
when the plastic strain is zero (also called the initial cohesion yield stress), 
is the angle made by the yield surface in the Rendulic plane at high values of 
(this angle is also called the dilation angle), and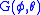 
is an appropriate function that is also smooth in the deviatoric stress plane.
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
(see yield surface
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
) describing the response of brittle materials such as concrete
Concrete
Concrete is a composite construction material, composed of cement and other cementitious materials such as fly ash and slag cement, aggregate , water and chemical admixtures.The word concrete comes from the Latin word...
, or rubble piles, to shear stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.
In Geotechnical Engineering
Geotechnical engineering
Geotechnical engineering is the branch of civil engineering concerned with the engineering behavior of earth materials. Geotechnical engineering is important in civil engineering, but is also used by military, mining, petroleum, or any other engineering concerned with construction on or in the ground...
it is used to define shear strength of soils and rocks at different effective stress
Effective stress
Karl von Terzaghi first proposed the relationship for effective stress in 1936. For him, the term ‘effective’ meant the calculated stress that was effective in moving soil, or causing displacements...
es.
In structural engineering
Structural engineering
Structural engineering is a field of engineering dealing with the analysis and design of structures that support or resist loads. Structural engineering is usually considered a specialty within civil engineering, but it can also be studied in its own right....
it is used to determine failure load as well as the angle of fracture
Fracture
A fracture is the separation of an object or material into two, or more, pieces under the action of stress.The word fracture is often applied to bones of living creatures , or to crystals or crystalline materials, such as gemstones or metal...
of a displacement fracture in concrete and similar materials. Coulomb
Charles-Augustin de Coulomb
Charles-Augustin de Coulomb was a French physicist. He is best known for developing Coulomb's law, the definition of the electrostatic force of attraction and repulsion. The [SI unit] of charge, the coulomb, was named after him....
's friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. Mohr's circle is used to determine which principal stresses that will produce this combination of shear and normal stress, and the angle of the plane in which this will occur. According to the principle of normality the stress introduced at failure will be perpendicular to the line describing the fracture condition.
It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the angle of friction. This makes the strength of the material determinable by comparing the external mechanical work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
the sum of these must be zero and this will make it possible to calculate the failure load of the construction.
A common improvement of this model is to combine Coulomb's friction hypothesis with Rankine's
William John Macquorn Rankine
William John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....
principal stress hypothesis to describe a separation fracture.
History of the development
The Mohr–Coulomb theory is named in honour of Charles-Augustin de CoulombCharles-Augustin de Coulomb
Charles-Augustin de Coulomb was a French physicist. He is best known for developing Coulomb's law, the definition of the electrostatic force of attraction and repulsion. The [SI unit] of charge, the coulomb, was named after him....
and Christian Otto Mohr. Coulomb's contribution was a 1776 essay entitled "Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l'architecture"
.
Mohr developed a generalised form of the theory around the end of the 19th century.
As the generalised form affected the interpretation of the criterion, but not the substance of it, some texts continue to refer to the criterion as simply the 'Coulomb criterion'.
Mohr–Coulomb failure criterion
The Mohr–Coulomb failure criterion represents the linear envelope that is obtained from a plot of the shear strength of a material versus the applied normal stress. This relation is expressed aswhere
is the shear strength, is the normal stress, is the intercept of the failure envelope with the axis, and is the slope of the failure envelope. The quantity is often called the cohesion and the angle is called the angle of internal friction . Compression is assumed to be positive in the following discussion. If compression is assumed to be negative then should be replaced with .If
, the Mohr–Coulomb criterion reduces to the Tresca criterion. On the other hand, if 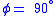the Mohr–Coulomb model is equivalent to the Rankine model. Higher values of are not allowed.From Mohr's circle we have
where
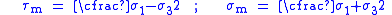
and
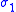is the maximum principal stress and is the minimum principal stress.Therefore the Mohr–Coulomb criterion may also be expressed as
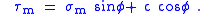
This form of the Mohr–Coulomb criterion is applicable to failure on a plane that is parallel to the
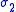direction.Mohr–Coulomb failure criterion in three dimensions
The Mohr–Coulomb criterion in three dimensions is often expressed asThe Mohr–Coulomb failure surface is a cone with a hexagonal cross section in deviatoric stress space.
The expressions for
and can be generalized to three dimensions by developing expressions for the normal stress and the resolved shear stress on a plane of arbitrary orientation with respect to the coordinate axes (basis vectors). If the unit normal to the plane of interest is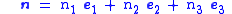where
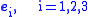are three orthonormal unit basis vectors, and if the principal stresses 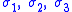are aligned with the basis vectors 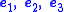, then the expressions for 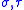are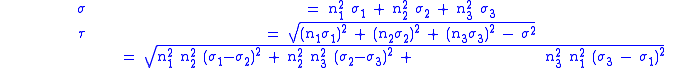The Mohr–Coulomb failure criterion can then be evaluated using the usual expression
for the six planes of maximum shear stress.
{| class="toccolours collapsible collapsed" width="60%" style="text-align:left"
!Derivation of normal and shear stress on a plane
|-
|Let the unit normal to the plane of interest be
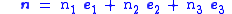
where
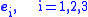are three orthonormal unit basis vectors. Then the traction vector on the plane is given byThe magnitude of the traction vector is given by
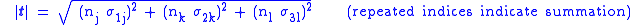
Then the magnitude of the stress normal to the plane is given by
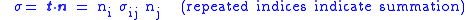
The magnitude of the resolved shear stress on the plane is given by
In terms of components, we have
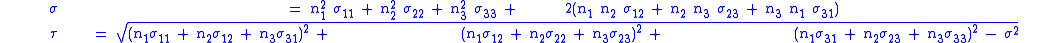
If the principal stresses
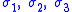are aligned with the basis vectors , then the expressions for are|}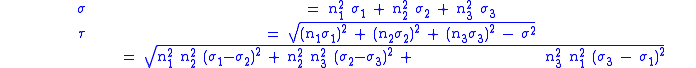
{| border="0"
|-
| valign="bottom"|
|
|
| valign="bottom"|
|-
|}
Mohr–Coulomb failure surface in Haigh–Westergaard space
The Mohr–Coulomb failure (yield) surface is often expressed in Haigh–Westergaad coordinates. For example, the functioncan be expressed as
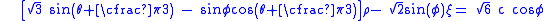
Alternatively, in terms of the invariants
we can writewhere
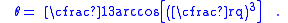
{| class="toccolours collapsible collapsed" width="80%" style="text-align:left"
!Derivation of alternative forms of Mohr–Coulomb yield function
|-
|We can express the yield function
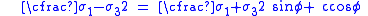
as
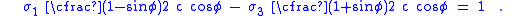
The Haigh–Westergaard invariants are related to the principal stresses by
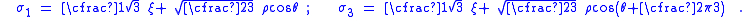
Plugging into the expression for the Mohr–Coulomb yield function gives us
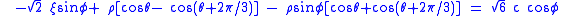
Using trigonometric identities for the sum and difference of cosines and rearrangement gives us the expression of the Mohr–Coulomb yield function in terms of
.We can express the yield function in terms of
by using the relationsand straightforward substitution.
|}
Mohr–Coulomb yield and plasticity
The Mohr–Coulomb yield surface is often used to model the plastic flow of geomaterials (and other cohesive-frictional materials). Many such materials show dilatational behavior under triaxial states of stress which the Mohr–Coulomb model does not include. Also, since the yield surface has corners, it may be inconvenient to use the original Mohr–Coulomb model to determine the direction of plastic flow (in the flow theory of plasticity).A common approach that is used is to use a non-associated plastic flow potential that is smooth. An example of such a potential is the function
where
is a parameter, is the value of when the plastic strain is zero (also called the initial cohesion yield stress), is the angle made by the yield surface in the Rendulic plane at high values of (this angle is also called the dilation angle), and 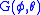is an appropriate function that is also smooth in the deviatoric stress plane.See also
- 3-D elasticity
- Byerlee's LawByerlee's lawByerlee's law is an experimentally derived law in physics that gives the stress circumstances in the Earth's crust at which fracturing along a geological fault takes place...
- Christian Otto Mohr
- Henri TrescaHenri TrescaHenri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
- Lateral earth pressureLateral earth pressureLateral earth pressure is the pressure that soil exerts against a structure in a sideways direction. The common applications of lateral earth pressure theory are for the design of ground engineering structures such as retaining walls, basements, tunnels, and to determine the friction on the sides...
- von Mises stressVon Mises stressThe von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J_2 reaches a critical value k. For this reason, it is sometimes called the J_2-plasticity or J_2 flow theory. It is part of a plasticity theory that applies best to ductile...
- Shear strengthShear strengthShear strength in engineering is a term used to describe the strength of a material or component against the type of yield or structural failure where the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is...
- Shear strength (soil)Shear strength (soil)Shear strength is a term used in soil mechanics to describe the magnitude of the shear stress that a soil can sustain. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding at particle contacts. Due to interlocking, particulate...
- Strain (materials science)Strain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
- Stress (physics)Stress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- Yield surfaceYield surfaceA yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
- Drucker Prager yield criterionDrucker Prager yield criterionThe Drucker–Prager yield criterion is a pressure-dependent model for determining whether a material has failed or undergone plastic yielding. The criterion was introduced to deal with the plastic deformation of soils...
— a smooth version of the M–C yield criterion