Shear strength (soil)
Encyclopedia
Shear strength is a term used in soil mechanics
to describe the magnitude of the shear stress
that a soil can sustain. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding at particle contacts. Due to interlocking, particulate material may expand or contract in volume as it is subject to shear strains. If soil expands its volume, the density of particles will decrease and the strength will decrease; in this case, the peak strength would be followed by a reduction of shear stress. The stress-strain relationship levels off when the material stops expanding or contracting, and when interparticle bonds are broken. The theoretical state at which the shear stress and density remain constant while the shear strain increases may be called the critical state, steady state, or residual strength.
The volume change behavior and interparticle friction depend on the density of the particles, the intergranular contact forces, and to a somewhat lesser extent, other factors such as the rate of shearing and the direction of the shear stress. The average normal intergranular contact force per unit area is called the effective stress
.
If water is not allowed to flow in or out of the soil, the stress path is called an undrained stress path. During undrained shear, if the particles are surrounded by a nearly incompressible fluid such as water, then the density of the particles cannot change without drainage, but the water pressure and effective stress will change. On the other hand, if the fluids are allowed to freely drain out of the pores, then the pore pressures will remain constant and the test path is called a drained stress path. The soil is free to dilate or contract during shear if the soil is drained. In reality, soil is partially drained, somewhere between the perfectly undrained and drained idealized conditions.
The shear strength of soil depends on the effective stress, the drainage conditions, the density of the particles, the rate of strain, and the direction of the strain.
For undrained, constant volume shearing, the Tresca
theory may be used to predict the shear strength, but for drained conditions, the Mohr–Coulomb theory
may be used.
Two important theories of soil shear are the critical state theory
and the steady state theory. There are key differences between the critical state condition and the steady state condition and the resulting theory corresponding to each of these conditions.
Conceptually, there is no such thing as the undrained strength of a soil. It depends on a number of factors, the main ones being:
Undrained strength is typically defined by Tresca theory, based on Mohr's circle as:
σ1 - σ3 = 2 Su
Where:
σ1 is the major principal stress
σ3 is the minor principal stress
is the shear strength (σ1 - σ3)/2
hence,
= Su (or sometimes cu), the undrained strength.
It is commonly adopted in limit equilibrium analyses where the rate of loading is very much greater than the rate at which pore water pressures, that are generated due to the action of shearing the soil, may dissipate. An example of this is rapid loading of sands during an earthquake, or the failure of a clay slope during heavy rain, and applies to most failures that occur during construction.
As an implication of undrained condition, no elastic
volumetric strains occur, and thus Poisson's ratio
is assumed to remain 0.5 throughout shearing. The Tresca soil model also assumes no plastic volumetric strains occur. This is of significance in more advanced analyses such as in finite element analysis. In these advanced analysis methods, soil models other than Tresca may be used to model the undrained condition including Mohr-Coulomb and critical state soil models such as the modified Cam-clay model, provided Poisson's ratio is maintained at 0.5.
One relationship used extensively by practicing engineers is the empirical observation that the ratio of the undrained shear strength c to the effective confining stress p' is approximately a constant for a given Over Consolidation Ratio (OCR), and varies linearly with the logarithm of the OCR. This idea was systematized in the empirical SHANSEP (stress history and normalized soil engineering properties) method.. This relationship can also be derived from both critical-state and steady-state soil mechanics .
in 1942.) combined it with the principle of effective stress.
In terms of effective stresses, the shear strength is often approximated by:
= σ' tan(φ') + c
Where σ' =(σ - u), is defined as the effective stress. σ is the total stress applied normal to the shear plane, and u is the pore water pressure acting on the same plane.
φ = the effective stress friction angle, or the'angle of internal friction' after Coulomb
friction
. The coefficient of friction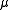
is equal to tan(φ'). Different values of friction angle can be defined, including the peak friction angle, φ'p, the critical state friction angle, φ'cv, or residual friction angle, φ'r.
c' = is called cohesion
, however, it usually arises as a consequence of forcing a straight line to fit through measured values of (τ,σ')even though the data actually falls on a curve. The intercept of the straight line on the shear stress axis is called the cohesion. It is well known that the resulting intercept depends on the range of stresses considered: it is not a fundamental soil property. The curvature (nonlinearity) of the failure envelope occurs because the dilatancy of closely packed soil particles depends on confining pressure.
The peak strength may occur before or at critical state, depending on the initial state of the soil particles being sheared:
The constant volume (or critical state) shear strength is said to be intrinsic to the soil, and independent of the initial density or packing arrangement of the soil grains. In this state the grains being sheared are said to be 'tumbling' over one another, with no significant granular interlock or sliding plane development affecting the resistance to shearing. At this point, no inherited fabric or bonding of the soil grains affects the soil strength.
The residual strength occurs for some soils where the shape of the particles that make up the soil become aligned during shearing (forming a slickenside
), resulting in reduced resistance to continued shearing (further strain softening). This is particularly true for most clays that comprise plate-like minerals, but is also observed in some granular soils with more elongate shaped grains. Clays that do not have plate-like minerals (like allophanic clays
) do not tend to exhibit residual strengths.
Use in practice: If one is to adopt critical state theory and take c' = 0;
p may be used, provided the level of anticipated strains are taken into account, and the effects of potential rupture or strain softening to critical state strengths are considered. For large strain deformation, the potential to form slickensided surface with a φ'r should be considered (such as pile driving).
The Critical State occurs at the quasi-static strain rate. It does not allow for differences in shear strength based on different strain rates. Also at the critical state, there is no particle alignment or specific soil structure.
The steady state strength is defined as the shear strength of the soil when it is at the steady state condition. The steady state condition is defined as "that state in which the mass is continuously deforming at constant volume, constant normal effective stress, constant shear stress, and constant velocity." Steve Poulos built off a hypothesis that Arthur Casagrande
was formulating towards the end of his career. Steady state based soil mechanics is sometimes called "Harvard soil mechanics". It is not the same as the "critical state" condition.
The steady state occurs only after all particle breakage if any is complete and all the particles are oriented in a statistically steady state condition and so that the shear stress needed to continue deformation at a constant velocity of deformation does not change. It applies to both the drained and the undrained case.
The steady state has a slightly different value depending on the strain rate at which it is measured. Thus the steady state shear strength at the quasi-static strain rate (the strain rate at which the critical state is defined to occur at) would seem to correspond to the critical state shear strength. However there is an additional difference between the two states. This is that at the steady state condition the grains position themselves in the steady state structure, whereas no such structure occurs for the critical state. In the case of shearing to large strains for soils with elongated particles, this steady state structure is one where the grains are oriented (perhaps even aligned) in the direction of shear. In the case where the particles are strongly aligned in the direction of shear, the steady state corresponds to the "residual condition."
Two common misconceptions regarding the steady state are that a) it is the same as the critical state and b) that it applies only to the undrained case. A primer on the Steady State theory can be found in a report by Poulos . Its use in earthquake engineering is described in detail in another publication by Poulos .
The difference between the steady state and the critical state is not merely one of semantics as is sometimes thought, and it is incorrect to use the two terms/concepts interchangeably. The additional requirements of the strict definition of the steady state over and above the critical state viz. a constant deformation velocity and statistically constant structure (the steady state structure), places the steady state condition within the framework of dynamical systems theory
. In fact, Joseph used this strict definition of the steady state to describe soil shear as a dynamical system.
Soil mechanics
Soil mechanics is a branch of engineering mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids, liquids, and gasses and other...
to describe the magnitude of the shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
that a soil can sustain. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding at particle contacts. Due to interlocking, particulate material may expand or contract in volume as it is subject to shear strains. If soil expands its volume, the density of particles will decrease and the strength will decrease; in this case, the peak strength would be followed by a reduction of shear stress. The stress-strain relationship levels off when the material stops expanding or contracting, and when interparticle bonds are broken. The theoretical state at which the shear stress and density remain constant while the shear strain increases may be called the critical state, steady state, or residual strength.
The volume change behavior and interparticle friction depend on the density of the particles, the intergranular contact forces, and to a somewhat lesser extent, other factors such as the rate of shearing and the direction of the shear stress. The average normal intergranular contact force per unit area is called the effective stress
Effective stress
Karl von Terzaghi first proposed the relationship for effective stress in 1936. For him, the term ‘effective’ meant the calculated stress that was effective in moving soil, or causing displacements...
.
If water is not allowed to flow in or out of the soil, the stress path is called an undrained stress path. During undrained shear, if the particles are surrounded by a nearly incompressible fluid such as water, then the density of the particles cannot change without drainage, but the water pressure and effective stress will change. On the other hand, if the fluids are allowed to freely drain out of the pores, then the pore pressures will remain constant and the test path is called a drained stress path. The soil is free to dilate or contract during shear if the soil is drained. In reality, soil is partially drained, somewhere between the perfectly undrained and drained idealized conditions.
The shear strength of soil depends on the effective stress, the drainage conditions, the density of the particles, the rate of strain, and the direction of the strain.
For undrained, constant volume shearing, the Tresca
Henri Tresca
Henri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
theory may be used to predict the shear strength, but for drained conditions, the Mohr–Coulomb theory
Mohr-Coulomb theory
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
may be used.
Two important theories of soil shear are the critical state theory
Critical state soil mechanics
Critical State Soil Mechanics is the area of Soil Mechanics that encompasses the conceptual models that represent the mechanical behavior of saturated remolded soils based on the Critical State concept.-Formulation:...
and the steady state theory. There are key differences between the critical state condition and the steady state condition and the resulting theory corresponding to each of these conditions.
Factors Controlling Shear Strength of Soils
The stress-strain relationship of soils, and therefore the shearing strength, is affected by:- soil composition (basic soil material): mineralogyMineralogyMineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...
, grain size and grain size distribution, shape of particles, pore fluid type and content, ionIonAn ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s on grain and in pore fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
. - state (initial): Defined by the initial void ratio, effective normal stress and shear stress (stress history). State can be described by terms such as: loose, dense, overconsolidated, normally consolidated, stiff, soft, contractive, dilative, etc.
- structure: Refers to the arrangement of particles within the soil mass; the manner the particles are packed or distributed. Features such as layers, joints, fissures, slickensides, voids, pockets, cementationCementationCementation may refer to:*Cementation , the process of deposition of dissolved mineral components in the interstices of sediments*Cementation , a small deposit of calcium, similar to a cyst...
, etc., are part of the structure. Structure of soils is described by terms such as: undisturbed, disturbed, remolded, compacted, cemented; flocculent, honey-combed, single-grained; flocculated, deflocculated; stratified, layered, laminated; isotropic and anisotropic. - Loading conditions: Effective stress path, i.e., drained, and undrained; and type of loading, i.e., magnitude, rate (static, dynamic), and time history (monotonic, cyclic).
Undrained strength
This term describes a type of shear strength in soil mechanics as distinct from drained strength.Conceptually, there is no such thing as the undrained strength of a soil. It depends on a number of factors, the main ones being:
- Orientation of stresses
- Stress path
- Rate of shearing
- Volume of material (like for fissured clays or rock mass)
Undrained strength is typically defined by Tresca theory, based on Mohr's circle as:
σ1 - σ3 = 2 Su
Where:
σ1 is the major principal stress
σ3 is the minor principal stress
is the shear strength (σ1 - σ3)/2hence,
= Su (or sometimes cu), the undrained strength.It is commonly adopted in limit equilibrium analyses where the rate of loading is very much greater than the rate at which pore water pressures, that are generated due to the action of shearing the soil, may dissipate. An example of this is rapid loading of sands during an earthquake, or the failure of a clay slope during heavy rain, and applies to most failures that occur during construction.
As an implication of undrained condition, no elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
volumetric strains occur, and thus Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
is assumed to remain 0.5 throughout shearing. The Tresca soil model also assumes no plastic volumetric strains occur. This is of significance in more advanced analyses such as in finite element analysis. In these advanced analysis methods, soil models other than Tresca may be used to model the undrained condition including Mohr-Coulomb and critical state soil models such as the modified Cam-clay model, provided Poisson's ratio is maintained at 0.5.
One relationship used extensively by practicing engineers is the empirical observation that the ratio of the undrained shear strength c to the effective confining stress p' is approximately a constant for a given Over Consolidation Ratio (OCR), and varies linearly with the logarithm of the OCR. This idea was systematized in the empirical SHANSEP (stress history and normalized soil engineering properties) method.. This relationship can also be derived from both critical-state and steady-state soil mechanics .
Drained shear strength
The drained shear strength is the shear strength of the soil when pore fluid pressures, generated during the course of shearing the soil, are able to dissipate during shearing. It also applies where no pore water exists in the soil (the soil is dry) and hence pore fluid pressures are negligible. It is commonly approximated using the Mohr-Coulomb equation. (It was called "Coulomb's equation" by Karl von TerzaghiKarl von Terzaghi
Karl von Terzaghi was an Austrian civil engineer and geologist, called the father of soil mechanics.-Early life:...
in 1942.) combined it with the principle of effective stress.
In terms of effective stresses, the shear strength is often approximated by:
= σ' tan(φ') + cWhere σ' =(σ - u), is defined as the effective stress. σ is the total stress applied normal to the shear plane, and u is the pore water pressure acting on the same plane.
φ = the effective stress friction angle, or the'angle of internal friction' after Coulomb
Charles-Augustin de Coulomb
Charles-Augustin de Coulomb was a French physicist. He is best known for developing Coulomb's law, the definition of the electrostatic force of attraction and repulsion. The [SI unit] of charge, the coulomb, was named after him....
friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
. The coefficient of friction
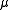is equal to tan(φ'). Different values of friction angle can be defined, including the peak friction angle, φ'p, the critical state friction angle, φ'cv, or residual friction angle, φ'r.c' = is called cohesion
Cohesion (geology)
Cohesion is the component of shear strength of a rock or soil that is independent of interparticle friction.In soils, true cohesion is caused by one of three things:# Electrostatic forces in stiff overconsolidated clays...
, however, it usually arises as a consequence of forcing a straight line to fit through measured values of (τ,σ')even though the data actually falls on a curve. The intercept of the straight line on the shear stress axis is called the cohesion. It is well known that the resulting intercept depends on the range of stresses considered: it is not a fundamental soil property. The curvature (nonlinearity) of the failure envelope occurs because the dilatancy of closely packed soil particles depends on confining pressure.
Critical state theory
A more advanced understanding of the behaviour of soil undergoing shearing lead to the development of the critical state theory of soil mechanics . In critical state soil mechanics, a distinct shear strength is identified where the soil undergoing shear does so at a constant volume, also called the 'critical state'. Thus there are three commonly identified shear strengths for a soil undergoing shear:- Peak strength
p - Critical state or constant volume strength
cv - Residual strength
r
The peak strength may occur before or at critical state, depending on the initial state of the soil particles being sheared:
- A loose soil will contract in volume on shearing, and may not develop any peak strength above critical state. In this case 'peak' strength will coincide with the critical state shear strength, once the soil has ceased contracting in volume. It may be stated that such soils do not exhibit a distinct 'peak strength'.
- A dense soil may contract slightly before granular interlock prevents further contraction (granular interlock is dependent on the shape of the grains and their initial packing arrangement). In order to continue shearing once granular interlock has occurred, the soil must dilate (expand in volume). As additional shear force is required to dilate the soil, a 'peak' strength occurs. Once this peak strength caused by dilation has been overcome through continued shearing, the resistance provided by the soil to the applied shear stress reduces (termed "strain softening"). Strain softening will continue until no further changes in volume of the soil occur on continued shearing. Peak strengths are also observed in overconsolidated clays where the natural fabric of the soil must be destroyed prior to reaching constant volume shearing. Other effects that result in peak strengths include cementation and bonding of particles.
The constant volume (or critical state) shear strength is said to be intrinsic to the soil, and independent of the initial density or packing arrangement of the soil grains. In this state the grains being sheared are said to be 'tumbling' over one another, with no significant granular interlock or sliding plane development affecting the resistance to shearing. At this point, no inherited fabric or bonding of the soil grains affects the soil strength.
The residual strength occurs for some soils where the shape of the particles that make up the soil become aligned during shearing (forming a slickenside
Slickenside
thumb|Slickensides on a sample of sandstone of the [[Juniata Formation]], from an outcrop on [[U.S. Route 322|Rt 322]] northeast of State College, Pennsylvania250px|thumb|left|How slickenfibre steps form and show sense of movement on a fault...
), resulting in reduced resistance to continued shearing (further strain softening). This is particularly true for most clays that comprise plate-like minerals, but is also observed in some granular soils with more elongate shaped grains. Clays that do not have plate-like minerals (like allophanic clays
Allophane
Allophane is a poorly-crystalline hydrous aluminium silicate clay mineraloid. Its chemical formula is Al2O3·1.3-2·2.5-3. Since it has short-range atomic order, it is a mineraloid, rather than a mineral, and can be identified by its distinctive infrared spectrum and its X-ray diffraction pattern. It...
) do not tend to exhibit residual strengths.
Use in practice: If one is to adopt critical state theory and take c' = 0;
p may be used, provided the level of anticipated strains are taken into account, and the effects of potential rupture or strain softening to critical state strengths are considered. For large strain deformation, the potential to form slickensided surface with a φ'r should be considered (such as pile driving).The Critical State occurs at the quasi-static strain rate. It does not allow for differences in shear strength based on different strain rates. Also at the critical state, there is no particle alignment or specific soil structure.
Steady state theory
A refinement of the critical state concept is the steady state concept.The steady state strength is defined as the shear strength of the soil when it is at the steady state condition. The steady state condition is defined as "that state in which the mass is continuously deforming at constant volume, constant normal effective stress, constant shear stress, and constant velocity." Steve Poulos built off a hypothesis that Arthur Casagrande
Arthur Casagrande
Arthur Casagrande was an Austrian-born American civil engineer who made important contributions to the fields of engineering geology and geotechnical engineering during its infancy...
was formulating towards the end of his career. Steady state based soil mechanics is sometimes called "Harvard soil mechanics". It is not the same as the "critical state" condition.
The steady state occurs only after all particle breakage if any is complete and all the particles are oriented in a statistically steady state condition and so that the shear stress needed to continue deformation at a constant velocity of deformation does not change. It applies to both the drained and the undrained case.
The steady state has a slightly different value depending on the strain rate at which it is measured. Thus the steady state shear strength at the quasi-static strain rate (the strain rate at which the critical state is defined to occur at) would seem to correspond to the critical state shear strength. However there is an additional difference between the two states. This is that at the steady state condition the grains position themselves in the steady state structure, whereas no such structure occurs for the critical state. In the case of shearing to large strains for soils with elongated particles, this steady state structure is one where the grains are oriented (perhaps even aligned) in the direction of shear. In the case where the particles are strongly aligned in the direction of shear, the steady state corresponds to the "residual condition."
Two common misconceptions regarding the steady state are that a) it is the same as the critical state and b) that it applies only to the undrained case. A primer on the Steady State theory can be found in a report by Poulos . Its use in earthquake engineering is described in detail in another publication by Poulos .
The difference between the steady state and the critical state is not merely one of semantics as is sometimes thought, and it is incorrect to use the two terms/concepts interchangeably. The additional requirements of the strict definition of the steady state over and above the critical state viz. a constant deformation velocity and statistically constant structure (the steady state structure), places the steady state condition within the framework of dynamical systems theory
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
. In fact, Joseph used this strict definition of the steady state to describe soil shear as a dynamical system.
See also
- Civil engineeringCivil engineeringCivil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
- Direct shear testDirect Shear TestA direct shear test also known as shearbox test is a laboratory or field test used by geotechnical engineers to measure the shear strength properties of soil or rock material, or of discontinuties in soil or rock masses.- Soil :...
- Dynamical systems theoryDynamical systems theoryDynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
- Earthworks (engineering)Earthworks (engineering)Earthworks are engineering works created through the moving or processing of quantities of soil or unformed rock.- Civil engineering use :Typical earthworks include roads, railway beds, causeways, dams, levees, canals, and berms...
- Effective stressEffective stressKarl von Terzaghi first proposed the relationship for effective stress in 1936. For him, the term ‘effective’ meant the calculated stress that was effective in moving soil, or causing displacements...
- Geotechnical engineeringGeotechnical engineeringGeotechnical engineering is the branch of civil engineering concerned with the engineering behavior of earth materials. Geotechnical engineering is important in civil engineering, but is also used by military, mining, petroleum, or any other engineering concerned with construction on or in the ground...
- Granular materialGranular materialA granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact . The constituents that compose granular material must be large enough such that they are not subject to thermal motion fluctuations...
- Publications in geotechnical engineering
- Soil mechanicsSoil mechanicsSoil mechanics is a branch of engineering mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids, liquids, and gasses and other...
- Triaxial shear test