Von Neumann's inequality
Encyclopedia
In operator theory
, von Neumann's inequality, due to John von Neumann
, states that, for a contraction
T acting on a Hilbert space
and a polynomial p, then the norm of p(T) is bounded by the supremum
of |p(z)| for z in the unit disk." In other words, for a fixed contraction T, the polynomial functional calculus map is itself a contraction. The inequality can be proved by considering the unitary dilation
of T, for which the inequality is obvious.
This inequality is a specific case of Matsaev's conjecture. That is that for any polynomial P and contraction T on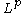
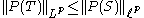
where S is the right-shift operator. The von Neumann inequality proves it true for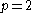
and for 
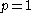and 
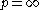it is true by straightforward calculation.
S.W. Drury has recently shown that the conjecture fails in the general case.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, von Neumann's inequality, due to John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, states that, for a contraction
Contraction (operator theory)
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling...
T acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and a polynomial p, then the norm of p(T) is bounded by the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of |p(z)| for z in the unit disk." In other words, for a fixed contraction T, the polynomial functional calculus map is itself a contraction. The inequality can be proved by considering the unitary dilation
Unitary dilation
In operator theory, a dilation of an operator T on a Hilbert space H is an operator on a larger Hilbert space K , whose restriction to H is T....
of T, for which the inequality is obvious.
This inequality is a specific case of Matsaev's conjecture. That is that for any polynomial P and contraction T on
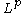
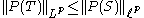
where S is the right-shift operator. The von Neumann inequality proves it true for
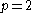and for 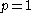and 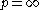it is true by straightforward calculation.S.W. Drury has recently shown that the conjecture fails in the general case.