Von Neumann cardinal assignment
Encyclopedia
The von Neumann cardinal assignment is a cardinal assignment
which uses ordinal number
s. For a well-order
ed set U, we define its cardinal number
to be the smallest ordinal number equinumerous to U. More precisely:
,
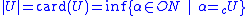where ON is the class of ordinals. This ordinal is also called the initial ordinal of the cardinal.
That such an ordinal exists and is unique is guaranteed by the fact that U is well-orderable and that the class of ordinals is well-ordered, using the axiom of replacement. With the full axiom of choice, every set is well-orderable, so every set has a cardinal; we order the cardinals using the inherited ordering from the ordinal numbers. This is readily found to coincide with the ordering via ≤c. This is a well-ordering of cardinal numbers.
, its cardinality, obtained by simply forgetting the order. Any well-ordered set having that ordinal as its order type
has the same cardinality. The smallest ordinal having a given cardinal as its cardinality is called the initial ordinal of that cardinal. Every finite ordinal (natural number) is initial, but most infinite ordinals are not initial. The axiom of choice is equivalent to the statement that every set can be well-ordered, i.e. that every cardinal has an initial ordinal. In this case, it is traditional to identify the cardinal number with its initial ordinal, and we say that the initial ordinal is a cardinal.
The α-th infinite initial ordinal is written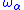
. Its cardinality is written ℵα (the α-th aleph number
). For example, the cardinality of ω0 = ω is ℵ0, which is also the cardinality of ω2, ωω, and ε0 (all are countable ordinals). So (assuming the axiom of choice) we identify ωα with ℵα, except that the notation ℵα is used for writing cardinals, and ωα for writing ordinals. This is important because arithmetic on cardinals is different from arithmetic on ordinals
, for example ℵα2 = ℵα whereas ωα2 > ωα. Also, ω1 is the smallest uncountable ordinal (to see that it exists, consider the set of equivalence classes of well-orderings of the natural numbers; each such well-ordering defines a countable ordinal, and ω1 is the order type of that set), ω2 is the smallest ordinal whose cardinality is greater than ℵ1, and so on, and ωω is the limit of ωn for natural numbers n (any limit of cardinals is a cardinal, so this limit is indeed the first cardinal after all the ωn).
Cardinal assignment
In set theory, the concept of cardinality is significantly developable without recourse to actually defining cardinal numbers as objects in theory itself...
which uses ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s. For a well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ed set U, we define its cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
to be the smallest ordinal number equinumerous to U. More precisely:
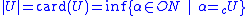,where ON is the class of ordinals. This ordinal is also called the initial ordinal of the cardinal.
That such an ordinal exists and is unique is guaranteed by the fact that U is well-orderable and that the class of ordinals is well-ordered, using the axiom of replacement. With the full axiom of choice, every set is well-orderable, so every set has a cardinal; we order the cardinals using the inherited ordering from the ordinal numbers. This is readily found to coincide with the ordering via ≤c. This is a well-ordering of cardinal numbers.
Initial ordinal of a cardinal
Each ordinal has an associated cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, its cardinality, obtained by simply forgetting the order. Any well-ordered set having that ordinal as its order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
has the same cardinality. The smallest ordinal having a given cardinal as its cardinality is called the initial ordinal of that cardinal. Every finite ordinal (natural number) is initial, but most infinite ordinals are not initial. The axiom of choice is equivalent to the statement that every set can be well-ordered, i.e. that every cardinal has an initial ordinal. In this case, it is traditional to identify the cardinal number with its initial ordinal, and we say that the initial ordinal is a cardinal.
The α-th infinite initial ordinal is written
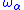. Its cardinality is written ℵα (the α-th aleph numberAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
). For example, the cardinality of ω0 = ω is ℵ0, which is also the cardinality of ω2, ωω, and ε0 (all are countable ordinals). So (assuming the axiom of choice) we identify ωα with ℵα, except that the notation ℵα is used for writing cardinals, and ωα for writing ordinals. This is important because arithmetic on cardinals is different from arithmetic on ordinals
Ordinal arithmetic
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
, for example ℵα2 = ℵα whereas ωα2 > ωα. Also, ω1 is the smallest uncountable ordinal (to see that it exists, consider the set of equivalence classes of well-orderings of the natural numbers; each such well-ordering defines a countable ordinal, and ω1 is the order type of that set), ω2 is the smallest ordinal whose cardinality is greater than ℵ1, and so on, and ωω is the limit of ωn for natural numbers n (any limit of cardinals is a cardinal, so this limit is indeed the first cardinal after all the ωn).