Cardinal assignment
Encyclopedia
In set theory
, the concept of cardinality is significantly developable without recourse to actually defining cardinal numbers as objects in theory itself (this is in fact a viewpoint taken by Frege
; Frege cardinals are basically equivalence classes on the entire universe of sets which are equinumerous). The concepts are developed by defining equinumerosity in terms of functions and the concepts of one-to-one
and onto
(injectivity and surjectivity); this gives us a pseudo-ordering relation
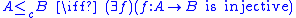
on the whole universe by size. It is not a true ordering because the trichotomy law need not hold: if both
and 
, it is true by the Cantor–Bernstein–Schroeder theorem
that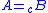
i.e. A and B are equinumerous, but they do not have to be literally equal; that at least one case holds turns out to be equivalent to the Axiom of choice.
Nevertheless, most of the interesting results on cardinality and its arithmetic can be expressed merely with =c.
The goal of a cardinal assignment is to assign to every set A a specific, unique set which is only dependent on the cardinality of A. This is in accordance with Cantor
's original vision of a cardinals: to take a set and abstract its elements into canonical "units" and collect these units into another set, such that the only thing special about this set is its size. These would be totally ordered by the relation
and =c would be true equality. As Y. N. Moschovakis says, however, this is mostly an exercise in mathematical elegance, and you don't gain much unless you are "allergic to subscripts." However, there are various valuable applications of "real" cardinal numbers in various models
of set theory.
In modern set theory, we usually use the Von Neumann cardinal assignment
which uses the theory of ordinal numbers and the full power of the Axioms of choice and replacement. Cardinal assignments do need the full Axiom of choice, if we want a decent cardinal arithmetic and an assignment for all sets.
. If the axiom of choice is not assumed we need to do something different. The oldest definition of the cardinality of a set X (implicit in Cantor and explicit in Frege and Principia Mathematica
) is as the set of all sets which are equinumerous with X: this does not work in ZFC or other related systems of axiomatic set theory because this collection is too large to be a set, but it does work in type theory
and in New Foundations
and related systems. However, if we restrict from this class to those equinumerous with X that have the least rank, then it will work (this is a trick due to Dana Scott
: it works because the collection of objects with any given rank is a set).
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the concept of cardinality is significantly developable without recourse to actually defining cardinal numbers as objects in theory itself (this is in fact a viewpoint taken by Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
; Frege cardinals are basically equivalence classes on the entire universe of sets which are equinumerous). The concepts are developed by defining equinumerosity in terms of functions and the concepts of one-to-one
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and onto
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
(injectivity and surjectivity); this gives us a pseudo-ordering relation
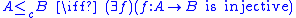
on the whole universe by size. It is not a true ordering because the trichotomy law need not hold: if both
and , it is true by the Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theorem
In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
that
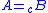i.e. A and B are equinumerous, but they do not have to be literally equal; that at least one case holds turns out to be equivalent to the Axiom of choice.Nevertheless, most of the interesting results on cardinality and its arithmetic can be expressed merely with =c.
The goal of a cardinal assignment is to assign to every set A a specific, unique set which is only dependent on the cardinality of A. This is in accordance with Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's original vision of a cardinals: to take a set and abstract its elements into canonical "units" and collect these units into another set, such that the only thing special about this set is its size. These would be totally ordered by the relation
and =c would be true equality. As Y. N. Moschovakis says, however, this is mostly an exercise in mathematical elegance, and you don't gain much unless you are "allergic to subscripts." However, there are various valuable applications of "real" cardinal numbers in various modelsModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of set theory.
In modern set theory, we usually use the Von Neumann cardinal assignment
Von Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
which uses the theory of ordinal numbers and the full power of the Axioms of choice and replacement. Cardinal assignments do need the full Axiom of choice, if we want a decent cardinal arithmetic and an assignment for all sets.
Cardinal assignment without the axiom of choice
Formally, assuming the axiom of choice, cardinality of a set X is the least ordinal α such that there is a bijection between X and α. This definition is known as the von Neumann cardinal assignmentVon Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
. If the axiom of choice is not assumed we need to do something different. The oldest definition of the cardinality of a set X (implicit in Cantor and explicit in Frege and Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
) is as the set of all sets which are equinumerous with X: this does not work in ZFC or other related systems of axiomatic set theory because this collection is too large to be a set, but it does work in type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and in New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
and related systems. However, if we restrict from this class to those equinumerous with X that have the least rank, then it will work (this is a trick due to Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
: it works because the collection of objects with any given rank is a set).