
Vorticity confinement
Encyclopedia
Vorticity confinement, a physics-based computational fluid dynamics
model analogous to shock capturing methods
, was invented by Dr. John Steinhoff
, professor at the University of Tennessee Space Institute, in the late 80s
to solve vortex
dominated flows.
It was first formulated to capture concentrated vortices shed from the wings, and later became popular in a wide range of research areas . During the 1990s and 2000s it became widely used in the field of engineering
.
approach which is extensively used in many condensed matter physics
applications. The effect of VC is to capture the small scale features over as few as 2 grid cells as they convect through the flow. The basic idea is similar to that of compression discontinuity
in Eulerian shock capturing methods
. The internal structure is maintained thin and so the details of the internal structure may not be important.
, modified using the confinement term, F: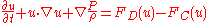
The discretized Euler equations with the extra term can be solved on fairly coarse grids, with simple low order accurate numerical methods, but still yield concentrated vortices which convect without spreading. VC has different forms, one of which is VC1
. It involves an added dissipation,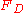 ,to the partial differential equation
,to the partial differential equation
, which when balanced with inward convection, , produce stable solutions. Another form is termed as VC2
, produce stable solutions. Another form is termed as VC2
in which dissipation
is balanced with nonlinear anti-diffusion to produce stable solitary wave
-like solutions.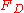 : Dissipation
: Dissipation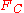 : Inward convection for VC1 and nonlinear anti-diffusion for VC2
: Inward convection for VC1 and nonlinear anti-diffusion for VC2
The main difference between VC1 and VC2 is that in the latter the centroid of the vortex
follows the local velocity moment
weighted by vorticity. This should provide greater accuracy than VC1 in cases where the convecting field is weak compared to the self induced velocity
of the vortex. One drawback is that VC2 is not as robust as VC1 because while VC1 involves convection like inward propagation of vorticity balanced by an outward second order diffusion, VC2 involves a second order inward propagation of vorticity balanced by 4th order outward dissipation
. This approach has been further extended to solve wave equation
and is called Wave confinement (WC).
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
model analogous to shock capturing methods
Shock capturing methods
In computational fluid dynamics, shock-capturing methods are a class of techniques for computing inviscid flows with shock waves. Computation of flow through shock waves is an extremely difficult task because such flows result in sharp, discontinuous changes in flow variables pressure, temperature,...
, was invented by Dr. John Steinhoff
John Steinhoff
John Steinhoff is a classical physicist, best known for his important contributions to computational fluid dynamics field. He invented a physics based method called vorticity confinement to compute the numerical solution of partial differential equations.- Biography :John studied at University of...
, professor at the University of Tennessee Space Institute, in the late 80s
to solve vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
dominated flows.
It was first formulated to capture concentrated vortices shed from the wings, and later became popular in a wide range of research areas . During the 1990s and 2000s it became widely used in the field of engineering
.
The method
VC has a basic familiarity to solitary waveSolitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
approach which is extensively used in many condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
applications. The effect of VC is to capture the small scale features over as few as 2 grid cells as they convect through the flow. The basic idea is similar to that of compression discontinuity
Discontinuity
Discontinuity may refer to:*Discontinuity , a harmless irregularity in a casting*Discontinuity in geotechnics is a plane or surface marking a change in physical or chemical properties in a soil or rock mass...
in Eulerian shock capturing methods
Shock capturing methods
In computational fluid dynamics, shock-capturing methods are a class of techniques for computing inviscid flows with shock waves. Computation of flow through shock waves is an extremely difficult task because such flows result in sharp, discontinuous changes in flow variables pressure, temperature,...
. The internal structure is maintained thin and so the details of the internal structure may not be important.
Example
Consider 2D Euler equationsEuler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
, modified using the confinement term, F:
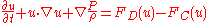
The discretized Euler equations with the extra term can be solved on fairly coarse grids, with simple low order accurate numerical methods, but still yield concentrated vortices which convect without spreading. VC has different forms, one of which is VC1
VC1
VC1 may refer to:* VC-1, a Microsoft SMPTE 421M video codec* Videocipher 1* First Vatican Council* Virtua Cop 1* VC-1A, the Brazilian Air Force One...
. It involves an added dissipation,
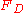 ,to the partial differential equation
,to the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, which when balanced with inward convection,
 , produce stable solutions. Another form is termed as VC2
, produce stable solutions. Another form is termed as VC2VC2
VC2 can represent:* Valkyria Chronicles II* Second Vatican Council* Virtua Cop 2* VideoCipher 2* VC-2, see Brazilian Air Force One...
in which dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
is balanced with nonlinear anti-diffusion to produce stable solitary wave
Solitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
-like solutions.
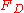 : Dissipation
: Dissipation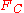 : Inward convection for VC1 and nonlinear anti-diffusion for VC2
: Inward convection for VC1 and nonlinear anti-diffusion for VC2The main difference between VC1 and VC2 is that in the latter the centroid of the vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
follows the local velocity moment
Moment
- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
weighted by vorticity. This should provide greater accuracy than VC1 in cases where the convecting field is weak compared to the self induced velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the vortex. One drawback is that VC2 is not as robust as VC1 because while VC1 involves convection like inward propagation of vorticity balanced by an outward second order diffusion, VC2 involves a second order inward propagation of vorticity balanced by 4th order outward dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
. This approach has been further extended to solve wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
and is called Wave confinement (WC).

