
Waterman polyhedron
Encyclopedia
Waterman polyhedra were invented around 1990 by the mathematician Steve Waterman.
Waterman polyhedra
are created by packing spheres according to the cubic close(st) packing (CCP), then sweeping away the spheres that are farther from the center than a defined radius. The resulting pack of spheres is then convex hull
ed, and thereby a polyhedron is created.
Waterman polyhedra form a vast family of polyhedra. Some of them have a number of nice properties such as multiple symmetries, or interesting and regular shapes. Others are just a collection of faces formed from irregular convex polygons.
The most popular Waterman polyhedra are those with centers at the point (0,0,0) and built out of hundreds of polygons. Such polyhedra resemble spheres. In fact, the more faces a Waterman polyhedron has, the more it resembles its circumscribed sphere
in volume and total area.
With each point of 3D space we can associate a family of Waterman polyhedra with different values of radii of the circumscribed spheres. Therefore, from a mathematical point of view we can consider Waterman polyhedra as a 4D space W(x, y, z, r), where x, y, z are coordinates of a point in 3D, and r is a positive number greater than 1.
Depending on the origin of the sweeping, a different shape and resulting polyhedron are obtained.
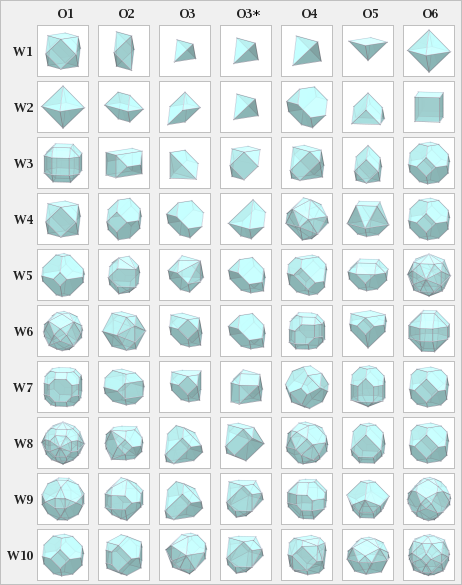
s and Archimedean solid
s. For this comparison of WP they are normalized, e.g. W2 O1 has a different size or volume than W1 O6, but has the same form as an octahedron.
Note: The W7 O1 might be mistaken for a truncated cuboctahedron
, as well W3 O1 = W12 O1 mistaken for a rhombicuboctahedron, but those WPs have two edge lengths and therefore don't qualify as Archimedean solids.
Included is a detailed analysis of the following 10 lattices - bcc, cuboctahedron, diamond, fcc, hcp, truncated octahedron, rhombic dodecahedron
, simple cubic, truncated tet tet, truncated tet truncated octahedron cuboctahedron.
Each of the 10 lattices were examined to isolate those particular origin points that manifested a
unique polyhedron, as well as possessing some minimal symmetry requirement. From a viable origin point, within a lattice, there exists an unlimited series of polyhedra. Given its proper sweep interval, then there is a one-to-one correspondence between each integer value
and a GWP.
Waterman polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
are created by packing spheres according to the cubic close(st) packing (CCP), then sweeping away the spheres that are farther from the center than a defined radius. The resulting pack of spheres is then convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
ed, and thereby a polyhedron is created.
Waterman polyhedra form a vast family of polyhedra. Some of them have a number of nice properties such as multiple symmetries, or interesting and regular shapes. Others are just a collection of faces formed from irregular convex polygons.
The most popular Waterman polyhedra are those with centers at the point (0,0,0) and built out of hundreds of polygons. Such polyhedra resemble spheres. In fact, the more faces a Waterman polyhedron has, the more it resembles its circumscribed sphere
Circumscribed sphere
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing...
in volume and total area.
With each point of 3D space we can associate a family of Waterman polyhedra with different values of radii of the circumscribed spheres. Therefore, from a mathematical point of view we can consider Waterman polyhedra as a 4D space W(x, y, z, r), where x, y, z are coordinates of a point in 3D, and r is a positive number greater than 1.
Seven origins of cubic close(st) packing (CCP)
There can be seven origins defined in CCP, where n = {1, 2, 3, …}:- Origin 1: offset 0,0,0, radius sqrt(2n)
- Origin 2: offset 1/2,1/2,0, radius sqrt(2+4n)/2
- Origin 3: offset 1/3,1/3,2/3, radius sqrt(6(n+1))/3
- Origin 3*: offset 1/3,1/3,1/3, radius sqrt(3+6n)/3
- Origin 4: offset 1/2,1/2,1/2, radius sqrt(3+8(n-1))/2
- Origin 5: offset 0,0,1/2, radius sqrt(1+4n)/2
- Origin 6: offset 1,0,0, radius sqrt(1+2(n-1))
Depending on the origin of the sweeping, a different shape and resulting polyhedron are obtained.

Waterman polyhedra and platonic / Archimedean solids
Interestingly some Waterman polyhedra (WP) actually create Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s and Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s. For this comparison of WP they are normalized, e.g. W2 O1 has a different size or volume than W1 O6, but has the same form as an octahedron.
Platonic solids
- W1 O3* = W2 O3* = W1 O3 = W1 O4 = tetrahedron
- W2 O1 = W1 O6 = octahedron
- W2 O6 = cube
- icosahedron and dodecahedron have no WP representation
Archimedean solids
- W1 O1 = W4 O1 = cuboctahedron
- W10 O1 = truncated octahedronTruncated octahedronIn geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
- W4 O3 = W2 O4 = truncated tetrahedronTruncated tetrahedronIn geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
- the others have no WP representation
Note: The W7 O1 might be mistaken for a truncated cuboctahedron
Truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
, as well W3 O1 = W12 O1 mistaken for a rhombicuboctahedron, but those WPs have two edge lengths and therefore don't qualify as Archimedean solids.
Generalized Waterman polyhedra (GWP)
Generalized Waterman polyhedra are defined as the convex hull derived from the point set of any spherical extraction from a regular lattice.Included is a detailed analysis of the following 10 lattices - bcc, cuboctahedron, diamond, fcc, hcp, truncated octahedron, rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, simple cubic, truncated tet tet, truncated tet truncated octahedron cuboctahedron.
Each of the 10 lattices were examined to isolate those particular origin points that manifested a
unique polyhedron, as well as possessing some minimal symmetry requirement. From a viable origin point, within a lattice, there exists an unlimited series of polyhedra. Given its proper sweep interval, then there is a one-to-one correspondence between each integer value
Integer-valued polynomial
In mathematics, an integer-valued polynomial P is a polynomial taking an integer value P for every integer n. Certainly every polynomial with integer coefficients is integer-valued. There are simple examples to show that the converse is not true: for example the polynomialgiving the triangle...
and a GWP.

