Weapon target assignment problem
Encyclopedia
The weapon target assignment problem (WTA) is a class of combinatorial optimization
problems present in the fields of optimization
and operations research
. It consists of finding an optimal assignment of a set of weapons of various types to a set of targets in order to maximize the total expected damage done to the opponent.
The basic problem is as follows:
Notice that as opposed to the classic assignment problem
or the generalized assignment problem
, more than one agent (i.e., weapon) can be assigned to each task (i.e., target) and not all targets are required to have weapons assigned. Thus, we see that the WTA allows one to formulate optimal assignment problems wherein tasks require cooperation among agents. Additionally, it provides the ability to model probabilistic completion of tasks in addition to costs.
Both static and dynamic versions of WTA can be considered. In the static case, the weapons are assigned to targets once. The dynamic case involves many rounds of assignment were the state of the system after each exchange of fire (round) in considered in the next round. While the majority of work has been done on the static WTA problem, recently the dynamic WTA problem has received more attention.
problem:
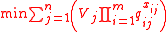
subject to the constraints
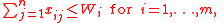
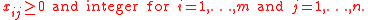
Where the variable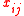
represents the assignment of as many weapons of type 
to target 
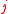and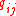 
is the probability of survival (
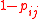). The first constraint requires that the number of weapons of each type assigned does not exceed the number available. The second constraint is the integral constraint.
Notice that minimizing the expected survival value is the same as maximizing the expected damage.
. Nonetheless, an exact solution can be found using branch and bound
techniques which utilize relaxation (approximation). Many heuristic algorithms have been proposed which provide near-optimal solutions in polynomial time .
|-
! Weapon Type !!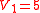
!! 
!! 
|-
| Tank || 0.3 || 0.2 || 0.05
|-
| Aircraft || 0.1 || 0.6 || 0.5
|-
| Sea Vessel || 0.4 || 0.5 || 0.4
|}
One feasible solution is to assign the sea vessel and one aircraft to the highest valued target (3). This results in an expected survival value of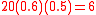
. One could then assign the remaining aircraft and 2 tanks to target #2, resulting in expected survival value of 
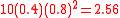. Finally, the remaining 3 tanks are assigned to target #1 which has an expected survival value of 
. Thus, we have a total expected survival value of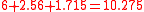 
.
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
problems present in the fields of optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
and operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
. It consists of finding an optimal assignment of a set of weapons of various types to a set of targets in order to maximize the total expected damage done to the opponent.
The basic problem is as follows:
- There are a number of weapons and a number of targets. The weapons are of type
. There are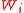 
available weapons of type 
. Similarly, there are 
targets, each with a value of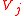 
. Any of the weapons can be assigned to any target. Each weapon type has a certain probability of destroying each target, given by 
.
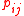Notice that as opposed to the classic assignment problem
Assignment problem
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics...
or the generalized assignment problem
Generalized assignment problem
In applied mathematics, the maximum generalized assignment problem is a problem in combinatorial optimization. This problem is a generalization of the assignment problem in which both tasks and agents have a size...
, more than one agent (i.e., weapon) can be assigned to each task (i.e., target) and not all targets are required to have weapons assigned. Thus, we see that the WTA allows one to formulate optimal assignment problems wherein tasks require cooperation among agents. Additionally, it provides the ability to model probabilistic completion of tasks in addition to costs.
Both static and dynamic versions of WTA can be considered. In the static case, the weapons are assigned to targets once. The dynamic case involves many rounds of assignment were the state of the system after each exchange of fire (round) in considered in the next round. While the majority of work has been done on the static WTA problem, recently the dynamic WTA problem has received more attention.
Formal mathematical definition
The weapon target assignment problem is often formulated as the following nonlinear integer programmingInteger programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
problem:
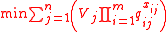
subject to the constraints
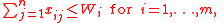
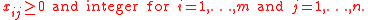
Where the variable
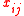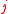represents the assignment of as many weapons of type to target and 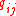is the probability of survival (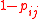). The first constraint requires that the number of weapons of each type assigned does not exceed the number available. The second constraint is the integral constraint.Notice that minimizing the expected survival value is the same as maximizing the expected damage.
Algorithms and generalizations
It has long been known that assignment problems are NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. Nonetheless, an exact solution can be found using branch and bound
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
techniques which utilize relaxation (approximation). Many heuristic algorithms have been proposed which provide near-optimal solutions in polynomial time .
Example
A commander has 5 tanks, 2 aircraft, and 1 sea vessel and is told to engage 3 targets with values 5, 10, and 20. Each weapon type has the following success probabilities against each target:-
- {| class="wikitable"
|-
! Weapon Type !!
!! !! |-
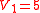| Tank || 0.3 || 0.2 || 0.05
|-
| Aircraft || 0.1 || 0.6 || 0.5
|-
| Sea Vessel || 0.4 || 0.5 || 0.4
|}
One feasible solution is to assign the sea vessel and one aircraft to the highest valued target (3). This results in an expected survival value of
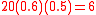. One could then assign the remaining aircraft and 2 tanks to target #2, resulting in expected survival value of 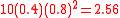. Finally, the remaining 3 tanks are assigned to target #1 which has an expected survival value of . Thus, we have a total expected survival value of 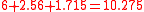.See also
- Auction algorithmAuction algorithmThe term "auction algorithm" applies to several variations of a combinatorial optimization algorithm which solves assignment problems, and network optimization problems with linear and convex/nonlinear cost. An auction algorithm has been used in a business setting to determine the best prices on a...
- Generalized assignment problemGeneralized assignment problemIn applied mathematics, the maximum generalized assignment problem is a problem in combinatorial optimization. This problem is a generalization of the assignment problem in which both tasks and agents have a size...
- Linear bottleneck assignment problemLinear bottleneck assignment problemIn combinatorial optimization, a field within mathematics, the linear bottleneck assignment problem is similar to the linear assignment problem. In plain words the problem is stated as follows:...
- Quadratic assignment problemQuadratic assignment problemThe quadratic assignment problem is one of fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems....
- Stable marriage problemStable marriage problemIn mathematics and computer science, the stable marriage problem is the problem of finding a stable matching between two sets of elements given a set of preferences for each element. A matching is a mapping from the elements of one set to the elements of the other set...