Wheeler-deWitt equation
Encyclopedia
In theoretical physics
, the Wheeler–DeWitt equation is a functional differential
equation. It is ill defined in the general case, but very important in theoretical physics
, especially in quantum gravity
. It is a functional differential equation on the space of three dimensional spatial metrics. The Wheeler–DeWitt equation has the form of an operator acting on a wave functional, the functional reduces to a function in cosmology. Contrary to the general case, the Wheeler–DeWitt equation is well defined in mini-superspaces like the configuration space of cosmological theories. An example of such a wave function is the Hartle–Hawking state. Bryce DeWitt
first published this equation in 1967 under the name "Einstein–Schrodinger equation"; it was later renamed the "Wheeler
–DeWitt equation".
Simply speaking, the Wheeler–DeWitt equation says
where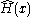
is the Hamiltonian constraint
in quantized general relativity
. Unlike ordinary quantum field theory or quantum mechanics, the Hamiltonian is a first class constraint
on physical states. We also have an independent constraint for each point in space.
Although the symbols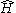
and 
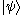may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics. 
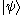is no longer a spatial wave function in the traditional sense of a complex-valued function that is defined on a 3-dimensional space-like surface and normalized to unity. Instead it is a functional
of field configurations on all of spacetime. This wave function contains all of the information about the geometry and matter content of the universe.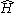
is still an operator that acts on the Hilbert space
of wave functions, but it is not the same Hilbert space as in the nonrelativistic case, and the Hamiltonian no longer determines evolution of the system, so the Schrödinger equation
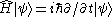no longer applies. This property is known as . The reemergence of time requires the tools of decoherence and clock operators.
We also need to augment the Hamiltonian constraint with momentum constraints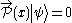
associated with spatial diffeomorphism invariance.
In minisuperspace
approximations, we only have one Hamiltonian constraint (instead of infinitely many of them).
In fact, the principle of general covariance
in general relativity implies that global evolution per se does not exist; the time
is just a label we assign to one of the coordinate axes. Thus, what we think about as time evolution of any physical system is just a gauge transformation, similar to that of QED
induced by U(1) local gauge transformation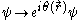
where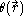 
plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the kernel of the Hamiltonian operator.
In general, the Hamiltonian
vanishes for a theory with general covariance or time-scaling invariance.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Wheeler–DeWitt equation is a functional differential
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
equation. It is ill defined in the general case, but very important in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, especially in quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. It is a functional differential equation on the space of three dimensional spatial metrics. The Wheeler–DeWitt equation has the form of an operator acting on a wave functional, the functional reduces to a function in cosmology. Contrary to the general case, the Wheeler–DeWitt equation is well defined in mini-superspaces like the configuration space of cosmological theories. An example of such a wave function is the Hartle–Hawking state. Bryce DeWitt
Bryce DeWitt
Bryce Seligman DeWitt was a theoretical physicist renowned for advancing gravity and field theories.-Biography:...
first published this equation in 1967 under the name "Einstein–Schrodinger equation"; it was later renamed the "Wheeler
John Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
–DeWitt equation".
Simply speaking, the Wheeler–DeWitt equation says
where
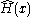is the Hamiltonian constraintHamiltonian constraint
In loop quantum gravity, dynamics such as time-evolutions of fields are controlled by the Hamiltonian constraint. The identity of the Hamiltonian constraint is a major open question in quantum gravity, as is extracting of physical observables from any such specific constraint.The Thiemann operator...
in quantized general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Unlike ordinary quantum field theory or quantum mechanics, the Hamiltonian is a first class constraint
First class constraint
In a constrained Hamiltonian system, a dynamical quantity is called a first class constraint if its Poisson bracket with all the other constraints vanishes on the constraint surface .-Poisson brackets:In Hamiltonian mechanics, consider a symplectic manifold M with a smooth Hamiltonian over...
on physical states. We also have an independent constraint for each point in space.
Although the symbols
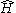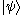and may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics. 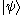is no longer a spatial wave function in the traditional sense of a complex-valued function that is defined on a 3-dimensional space-like surface and normalized to unity. Instead it is a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of field configurations on all of spacetime. This wave function contains all of the information about the geometry and matter content of the universe.
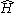is still an operator that acts on the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of wave functions, but it is not the same Hilbert space as in the nonrelativistic case, and the Hamiltonian no longer determines evolution of the system, so the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
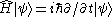no longer applies. This property is known as . The reemergence of time requires the tools of decoherence and clock operators.We also need to augment the Hamiltonian constraint with momentum constraints
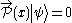
associated with spatial diffeomorphism invariance.
In minisuperspace
Minisuperspace
In quantum gravity, the phase space is infinite dimensional as we are dealing with a field theory. An approximation which is sometimes taken is to only consider the largest wavelength modes of the order of the size of the universe when studying cosmological models. This is the minisuperspace...
approximations, we only have one Hamiltonian constraint (instead of infinitely many of them).
In fact, the principle of general covariance
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
in general relativity implies that global evolution per se does not exist; the time
is just a label we assign to one of the coordinate axes. Thus, what we think about as time evolution of any physical system is just a gauge transformation, similar to that of QEDQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
induced by U(1) local gauge transformation
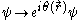where 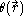plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the kernel of the Hamiltonian operator.In general, the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
vanishes for a theory with general covariance or time-scaling invariance.