Whitehead product
Encyclopedia
In mathematics, the Whitehead product is a graded
quasi-Lie algebra
structure on the homotopy group
s of a space. It was defined by J. H. C. Whitehead
in .
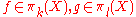, the Whitehead bracket
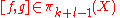
is defined as follows:
The product
can be obtained by attaching a 
-cell to the wedge sum
;
the attaching map is a map
Represent
and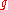 
by maps
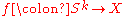
and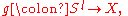
then compose their wedge with the attaching map, as
The homotopy class of the resulting map does not depend on the choices of representatives, and thus one obtains a well-defined element of
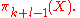
s), so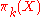
has degree 
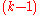; equivalently, 
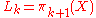(setting L to be the graded quasi-Lie algebra). Thus 
acts on each graded component.
, and is thus a graded
quasi-Lie algebra
; this is proven in via the Massey triple product
.
If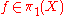
, then the Whitehead bracket is related to the usual conjugation action of 
on 
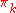by
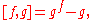
where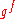
denotes the conjugation
of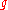
by 
.
For
, this reduces to
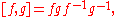
which is the usual commutator.
The relevant MSC
code is: 55Q15, Whitehead products and generalizations.
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
quasi-Lie algebra
Quasi-Lie algebra
In mathematics, a quasi-Lie algebra in abstract algebra is just like a Lie algebra, but with the usual axiom[x,x]=0replaced by[x,y]=-[y,x] ....
structure on the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of a space. It was defined by J. H. C. Whitehead
J. H. C. Whitehead
John Henry Constantine Whitehead FRS , known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai , in India, and died in Princeton, New Jersey, in 1960....
in .
Definition
Given elements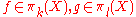, the Whitehead bracket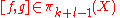is defined as follows:
The product
can be obtained by attaching a -cell to the wedge sumWedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
;the attaching map is a map
Represent
and 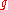by maps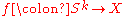and
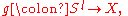
then compose their wedge with the attaching map, as
The homotopy class of the resulting map does not depend on the choices of representatives, and thus one obtains a well-defined element of
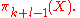
Grading
Note that there is a shift of 1 in the grading (compared to the indexing of homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s), so
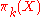has degree 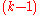; equivalently, 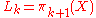(setting L to be the graded quasi-Lie algebra). Thus acts on each graded component.Properties
The Whitehead product is bilinear, graded-symmetric, and satisfies the graded Jacobi identityGraded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
, and is thus a graded
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
quasi-Lie algebra
Quasi-Lie algebra
In mathematics, a quasi-Lie algebra in abstract algebra is just like a Lie algebra, but with the usual axiom[x,x]=0replaced by[x,y]=-[y,x] ....
; this is proven in via the Massey triple product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
.
If
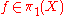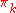, then the Whitehead bracket is related to the usual conjugation action of on by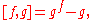where
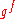denotes the conjugationInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
of
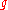by .For
, this reduces to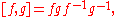which is the usual commutator.
The relevant MSC
Mathematics Subject Classification
The Mathematics Subject Classification is an alphanumerical classification scheme collaboratively produced by staff of and based on the coverage of the two major mathematical reviewing databases, Mathematical Reviews and Zentralblatt MATH...
code is: 55Q15, Whitehead products and generalizations.