
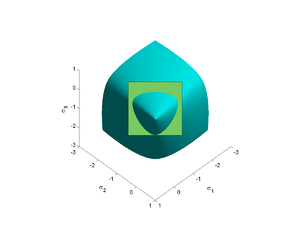
Willam-Warnke yield criterion
Encyclopedia
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
is a function that is used to predict when failure will occur in concrete
Concrete
Concrete is a composite construction material, composed of cement and other cementitious materials such as fly ash and slag cement, aggregate , water and chemical admixtures.The word concrete comes from the Latin word...
and other cohesive-frictional materials such as rock
Rock (geology)
In geology, rock or stone is a naturally occurring solid aggregate of minerals and/or mineraloids.The Earth's outer solid layer, the lithosphere, is made of rock. In general rocks are of three types, namely, igneous, sedimentary, and metamorphic...
, soil
Soil
Soil is a natural body consisting of layers of mineral constituents of variable thicknesses, which differ from the parent materials in their morphological, physical, chemical, and mineralogical characteristics...
, and ceramic
Ceramic
A ceramic is an inorganic, nonmetallic solid prepared by the action of heat and subsequent cooling. Ceramic materials may have a crystalline or partly crystalline structure, or may be amorphous...
s. This yield criterion has the functional form
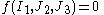
where
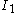 is the first invariant of the Cauchy stress tensor, and
is the first invariant of the Cauchy stress tensor, and 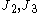 are the second and third invariants of the deviatoric part of the Cauchy stress tensor. There are three material parameters (
are the second and third invariants of the deviatoric part of the Cauchy stress tensor. There are three material parameters (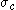 - the uniaxial compressive strength,
- the uniaxial compressive strength, 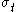 - the uniaxial tensile strength,
- the uniaxial tensile strength, 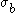 - the equibiaxial compressive strength) that have to be determined before the Willam-Warnke yield criterion may be applied to predict failure.
- the equibiaxial compressive strength) that have to be determined before the Willam-Warnke yield criterion may be applied to predict failure.In terms of
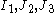 , the Willam-Warnke yield criterion can be expressed as
, the Willam-Warnke yield criterion can be expressed as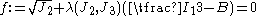
where
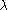 is a function that depends on
is a function that depends on 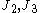 and the three material parameters and
and the three material parameters and 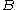 depends only on the material parameters. The function
depends only on the material parameters. The function 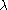 can be interpreted as the friction angle which depends on the Lode angle (
can be interpreted as the friction angle which depends on the Lode angle (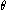 ). The quantity
). The quantity 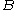 is interpreted as a cohesion pressure. The Willam-Warnke yield criterion may therefore be viewed as a combination of the Mohr-Coulomb
is interpreted as a cohesion pressure. The Willam-Warnke yield criterion may therefore be viewed as a combination of the Mohr-CoulombMohr-Coulomb theory
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
and the Drucker-Prager yield criteria.
Willam-Warnke yield function
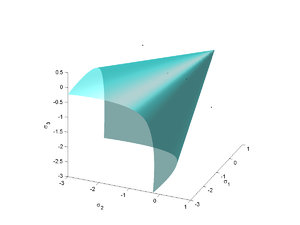
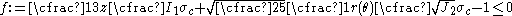
where
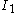 is the first invariant of the stress tensor,
is the first invariant of the stress tensor, 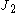 is the second invariant of the deviatoric part of the stress tensor,
is the second invariant of the deviatoric part of the stress tensor, 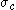 is the yield stress in uniaxial compression, and
is the yield stress in uniaxial compression, and 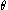 is the Lode angle given by
is the Lode angle given by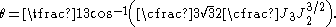
The locus of the boundary of the stress surface in the deviatoric stress plane is expressed in polar coordinates by the quantity
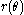 which is given by
which is given by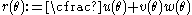
where
The quantities
 and
and  describe the position vectors at the locations
describe the position vectors at the locations  and can be expressed in terms of
and can be expressed in terms of  as
as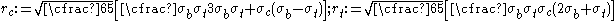
The parameter
 in the model is given by
in the model is given by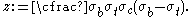
The Haigh-Westergaard representation
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
of the Willam-Warnke yield condition can be
written as
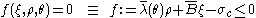
where
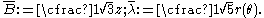
Modified forms of the Willam-Warnke yield criterion
An alternative form of the Willam-Warnke yield criterion in Haigh-Westergaard coordinatesYield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
is the Ulm-Coussy-Bazant form :
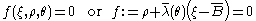
where
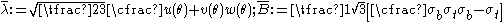
and
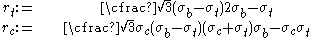
The quantities
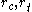 are interpreted as friction coefficients. For the yield surface to be convex, the Willam-Warnke yield criterion requires that
are interpreted as friction coefficients. For the yield surface to be convex, the Willam-Warnke yield criterion requires that 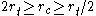 and
and 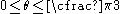 .
.
External links
- Kaspar Willam and E.P. Warnke (1974). Constitutive model for the triaxial behavior of concrete
- Palko, J. L. (1993). Interactive reliability model for whisker-toughened ceramics
- The ‘‘Chunnel’’ Fire. I: Chemoplastic softening in rapidly heated concrete by Franz-Josef Ulm, Olivier Coussy, and Zdeneˇk P. Bazˇant.

