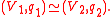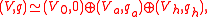Witt's theorem
Encyclopedia
Witt theorem, named after Ernst Witt
, is a basic result in the algebraic theory of quadratic form
s: any isometry
between two subspaces of a nonsingular quadratic space over a field k may be extended to an isometry of the whole space. An analogous statement holds also for skew-symmetric, Hermitian and skew-Hermitian bilinear forms over arbitrary fields. The theorem applies to classification of quadratic forms over k and in particular allows one to define the Witt group
W(k) which controls the "stable" theory of quadratic forms over the field k.
between two subspaces of V then f extends to an isometry of V.
Witt's theorem implies that the dimension of a maximal isotropic subspace of V is an invariant, called the index or of b, and moreover, that the isometry group
of (V, b) acts
transitively on the set of maximal isotropic subspaces. This fact plays an important role in the structure theory and representation theory
of the isometry group and in the theory of reductive dual pair
s.
Then the quadratic spaces (V1, q1) and (V2, q2) are isometric:
In other words, the direct summand (V, q) appearing in both sides of an isomorphism between quadratic spaces may be "cancelled".
it admits a Witt decomposition:
where V0=ker q is the radical of q, (Va, qa) is an anisotropic quadratic space and (Vh, qh) is a hyperbolic quadratic space. Moreover, the anisotropic summand and the hyperbolic summand in a Witt decomposition of (V, q) are determined uniquely up to isomorphism.
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
, is a basic result in the algebraic theory of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s: any isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
between two subspaces of a nonsingular quadratic space over a field k may be extended to an isometry of the whole space. An analogous statement holds also for skew-symmetric, Hermitian and skew-Hermitian bilinear forms over arbitrary fields. The theorem applies to classification of quadratic forms over k and in particular allows one to define the Witt group
Witt group
In mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.-Definition:Fix a field k. All vector spaces will be assumed to be finite-dimensional...
W(k) which controls the "stable" theory of quadratic forms over the field k.
Statement of the theorem
Let (V, b) be a finite-dimensional vector space over an arbitrary field k together with a nondegenerate symmetric or skew-symmetric bilinear form. If f: U→U' is an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
between two subspaces of V then f extends to an isometry of V.
Witt's theorem implies that the dimension of a maximal isotropic subspace of V is an invariant, called the index or of b, and moreover, that the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of (V, b) acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
transitively on the set of maximal isotropic subspaces. This fact plays an important role in the structure theory and representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the isometry group and in the theory of reductive dual pair
Reductive dual pair
In the mathematical field of representation theory, a reductive dual pair is a pair of subgroups of the isometry group Sp of a symplectic vector space W, such that G is the centralizer of G ′ in Sp and vice versa, and these groups act reductively on W...
s.
Witt's cancellation theorem
Let (V, q), (V1, q1), (V2, q2) be three quadratic spaces over a field k. Assume thatThen the quadratic spaces (V1, q1) and (V2, q2) are isometric:
In other words, the direct summand (V, q) appearing in both sides of an isomorphism between quadratic spaces may be "cancelled".
Witt's decomposition theorem
Let (V, q) be a quadratic space over a field k. Thenit admits a Witt decomposition:
where V0=ker q is the radical of q, (Va, qa) is an anisotropic quadratic space and (Vh, qh) is a hyperbolic quadratic space. Moreover, the anisotropic summand and the hyperbolic summand in a Witt decomposition of (V, q) are determined uniquely up to isomorphism.