Wold's theorem
Encyclopedia
In statistics
, Wold's decomposition or the Wold representation theorem (not to be confused with the Wold theorem that is the discrete-time analog of the Wiener–Khinchine theorem) named after Herman Wold
, says that every covariance-stationary
time series
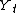can be written as an infinite moving average
(MA(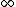
)) process of its innovation process. Such a formulation is known as a moving average representation for the time series, not to be confused with a simple running mean of data series.
Formally
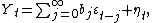
where:
Note that the moving average coefficients have these properties:
This theorem can be considered as an existence theorem: any stationary process has this seemingly special representation. Not only is the existence of such a simple linear and exact representation remarkable, but even more so is the special nature of the moving average model. Imagine creating a process that is a moving average but not satisfying these properties 1–4. For example, the coefficients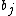
could define an acausal and non-minimum delay model. Nevertheless the theorem assures the existence of a causal minimum delay moving average that exactly represents this process. How this all works for the case of causality and the minimum delay property is discussed in Scargle (1981), where an extension of the Wold Decomposition is discussed.
The usefulness of the Wold Theorem is that it allows the dynamic
evolution of a variable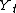
to be approximated by a linear model
. If the innovations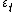
are independent
, then the linear model is the only possible representation relating the observed value of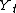
to its past evolution. However, when 
is merely an uncorrelated
but not independent sequence, then the linear model exists but it is not the only representation of the dynamic dependence of the series. In this latter case, it is possible that the linear model may not be very useful, and there would be a nonlinear model relating the observed value of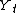
to its past evolution. However, in practical time series analysis, it often the case that only linear predictors are considered, partly on the grounds of simplicity, in which case the Wold decomposition is directly relevant.
The Wold representation depends on an infinite number of parameters, although in practice they usually decay rapidly. The autoregressive model
is an alternative that may have only a few coefficients if the corresponding moving average has many. These two models can be combined into an autoregressive-moving average (ARMA) model
, or an autoregressive-integrated-moving average (ARIMA) model if non-stationarity is involved. See Scargle(1981) and references there.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Wold's decomposition or the Wold representation theorem (not to be confused with the Wold theorem that is the discrete-time analog of the Wiener–Khinchine theorem) named after Herman Wold
Herman Wold
Herman Ole Andreas Wold was a Norwegian-born econometrician and statistician who had a long career in Sweden...
, says that every covariance-stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
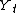can be written as an infinite moving averageMoving average model
In time series analysis, the moving-average model is a common approach for modeling univariate time series models. The notation MA refers to the moving average model of order q:...
(MA(
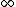)) process of its innovation process. Such a formulation is known as a moving average representation for the time series, not to be confused with a simple running mean of data series.Formally
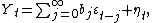
where:
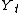is the time seriesTime seriesIn statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
being considered,
is an uncorrelated sequence which is the innovation process to the process 
– that is, a white noise process that is input to the linear filter {
}.
is the possibly infinite vector of moving average weights (coefficients or parameters)
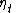is a deterministic component, which is zero in the absence of trends in 
.
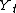Note that the moving average coefficients have these properties:
- Stable, that is absolutely summable
< 
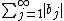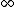
- Causal (i.e. there are no terms with j < 0)
- Minimum delay
- Constant (
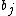independent of t) - It is conventional to define
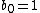
This theorem can be considered as an existence theorem: any stationary process has this seemingly special representation. Not only is the existence of such a simple linear and exact representation remarkable, but even more so is the special nature of the moving average model. Imagine creating a process that is a moving average but not satisfying these properties 1–4. For example, the coefficients
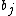could define an acausal and non-minimum delay model. Nevertheless the theorem assures the existence of a causal minimum delay moving average that exactly represents this process. How this all works for the case of causality and the minimum delay property is discussed in Scargle (1981), where an extension of the Wold Decomposition is discussed.The usefulness of the Wold Theorem is that it allows the dynamic
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
evolution of a variable
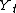to be approximated by a linear modelLinear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
. If the innovations
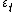are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, then the linear model is the only possible representation relating the observed value of
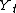to its past evolution. However, when is merely an uncorrelatedUncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
but not independent sequence, then the linear model exists but it is not the only representation of the dynamic dependence of the series. In this latter case, it is possible that the linear model may not be very useful, and there would be a nonlinear model relating the observed value of
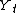to its past evolution. However, in practical time series analysis, it often the case that only linear predictors are considered, partly on the grounds of simplicity, in which case the Wold decomposition is directly relevant.The Wold representation depends on an infinite number of parameters, although in practice they usually decay rapidly. The autoregressive model
Autoregressive model
In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
is an alternative that may have only a few coefficients if the corresponding moving average has many. These two models can be combined into an autoregressive-moving average (ARMA) model
Autoregressive moving average model
In statistics and signal processing, autoregressive–moving-average models, sometimes called Box–Jenkins models after the iterative Box–Jenkins methodology usually used to estimate them, are typically applied to autocorrelated time series data.Given a time series of data Xt, the ARMA model is a...
, or an autoregressive-integrated-moving average (ARIMA) model if non-stationarity is involved. See Scargle(1981) and references there.