Word (group theory)
Encyclopedia
In group theory
, a word is any written product of group
elements and their inverses. For example, if x, y and z are elements of a group G, then xy, z-1xzz and y-1zxx-1yz-1 are words in the set {x, y, z}. Words play an important role in the theory of free group
s and presentations
, and are central objects of study in combinatorial group theory
.
of G. A word in S is any expression of the form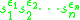
where s1,...,sn are elements of S and each εi is ±1. The number n is known as the length of the word.
Each word in S represents an element of G, namely the product of the expression. By convention, the identity element can be represented by the empty word, which is the unique word of length zero.
notation as an abbreviation. For example, the word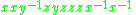
could be written as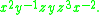
This latter expression is not a word itself—it is simply a shorter notation for the original.
When dealing with long words, it can be helpful to use an overline
to denote inverses of elements of S. Using overline notation, the above word would be written as follows: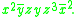
if every element of G can be represented by a word in S. If S is a generating set, a relation is a pair of words in S that represent the same element of G. These are usually written as equations: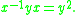
A set
of relations defines G if every relation in G follows logically from those in 
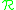, using the axioms for a group. A presentation for G is a pair 
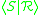, where S is a generating set for G and 
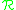is a defining set of relations.
For example, the Klein four-group
can be defined by the presentation
Here 1 denotes the empty word, which represents the identity element.
When S is not a generating set for G, the set of elements represented by words in S is a subgroup
of G. This is known as the subgroup of G generated by S, and is usually denoted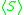
. It is the smallest subgroup of G that contains the elements of S.
This operation is known as reduction, and it does not change the group element represented by the word. (Reductions can be thought of as relations that follow from the group axioms.)
A reduced word is a word that contains no redundant pairs. Any word can be simplified to a reduced word by performing a sequence of reductions: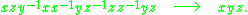
The result does not depend on the order in which the reductions are performed.
If S is any set, the free group
over S is the group with presentation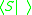
. That is, the free group over S is the group generated by the elements of S, with no extra relations. Every element of the free group can be written uniquely as a reduced word in S.
A word is cyclically reduced if and only if
every cyclic permutation
of the word is reduced.
Even if the two words are reduced, the product may not be.
The inverse of a word is obtained by inverting each generator, and switching the order of the elements: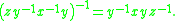
The product of a word with its inverse can be reduced to the empty word: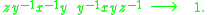
You can move a generator from the beginning to the end of a word by conjugation: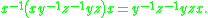
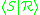for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn
in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable
.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a word is any written product of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
elements and their inverses. For example, if x, y and z are elements of a group G, then xy, z-1xzz and y-1zxx-1yz-1 are words in the set {x, y, z}. Words play an important role in the theory of free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s and presentations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
, and are central objects of study in combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
.
Definition
Let G be a group, and let S be a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of G. A word in S is any expression of the form
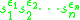
where s1,...,sn are elements of S and each εi is ±1. The number n is known as the length of the word.
Each word in S represents an element of G, namely the product of the expression. By convention, the identity element can be represented by the empty word, which is the unique word of length zero.
Notation
When writing words, it is common to use exponentialExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
notation as an abbreviation. For example, the word
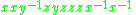
could be written as
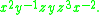
This latter expression is not a word itself—it is simply a shorter notation for the original.
When dealing with long words, it can be helpful to use an overline
Overline
An overline or overbar or overscore , refers to the typographical feature of a line drawn immediately above the text, for example used to indicate medieval sigla. Specifically, a line drawn over one symbol is a macron, and a line over a collection of symbols is a vinculum...
to denote inverses of elements of S. Using overline notation, the above word would be written as follows:
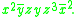
Words and presentations
A subset S of a group G is called a generating setGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
if every element of G can be represented by a word in S. If S is a generating set, a relation is a pair of words in S that represent the same element of G. These are usually written as equations:
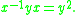
A set
of relations defines G if every relation in G follows logically from those in 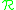, using the axioms for a group. A presentation for G is a pair 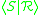, where S is a generating set for G and 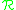is a defining set of relations.For example, the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
can be defined by the presentation
Here 1 denotes the empty word, which represents the identity element.
When S is not a generating set for G, the set of elements represented by words in S is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. This is known as the subgroup of G generated by S, and is usually denoted
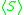. It is the smallest subgroup of G that contains the elements of S.Reduced words
Any word in which a generator appears next to its own inverse (xx-1 or x-1x) can be simplified by omitting the redundant pair:This operation is known as reduction, and it does not change the group element represented by the word. (Reductions can be thought of as relations that follow from the group axioms.)
A reduced word is a word that contains no redundant pairs. Any word can be simplified to a reduced word by performing a sequence of reductions:
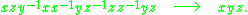
The result does not depend on the order in which the reductions are performed.
If S is any set, the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
over S is the group with presentation
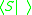. That is, the free group over S is the group generated by the elements of S, with no extra relations. Every element of the free group can be written uniquely as a reduced word in S.A word is cyclically reduced if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
every cyclic permutation
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
of the word is reduced.
Normal forms
A normal form for a group G with generating set S is a choice of one reduced word in S for each element of G. For example:- The words 1, i, j, ij are a normal form for the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. - The words 1, r, r2, ..., rn-1, s, sr, ..., srn-1 are a normal form for the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dihn. - The set of reduced words in S are a normal form for the free group over S.
- The set of words of the form xmyn for m,n ∈ Z are a normal form for the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s 〈x〉 and 〈y〉.
Operations on words
The product of two words is obtained by concatenation:Even if the two words are reduced, the product may not be.
The inverse of a word is obtained by inverting each generator, and switching the order of the elements:
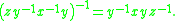
The product of a word with its inverse can be reduced to the empty word:
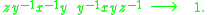
You can move a generator from the beginning to the end of a word by conjugation:
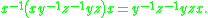
The word problem
Given a presentation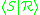 for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max DehnMax Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
.