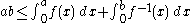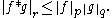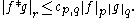Young's inequality
Encyclopedia
In mathematics
, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution
of two functions. They are named for William Henry Young
.
Young's inequality for products can be used to prove Hölder's inequality
. It is also used widely to estimate the norm of nonlinear terms in PDE theory
, since it allows one to estimate a product of two terms by a sum of the same terms raised to a power and scaled.
s and p and q are positive real numbers such that 1/p + 1/q = 1, then
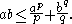
Equality holds if and only if ap = bq. This form of Young's inequality is a special case of the inequality of weighted arithmetic and geometric means and can be used to prove Hölder's inequality
.
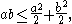
which also gives rise to the so-called Young's inequality with ε (valid for any ε > 0), sometimes called the Peter-Paul inequality:
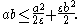
 For the standard version of the inequality,
For the standard version of the inequality,
let f denote a real-valued, continuous and strictly increasing function on [0, c] with c > 0 and f(0) = 0. Let f−1 denote the inverse function
of f. Then, for all a ∈ [0, c] and b ∈ [0, f(c)],
with equality if and only if b = f(a).
and its Legendre transform (convex conjugate
) is denoted by g, then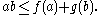
This follows immediately from the definition of the Legendre transform. This inequality also holds — in the form a ·b ≤ f(a) + g(b) — if f is a convex function taking a vector argument .
, the following result is also called Young's inequality:
Suppose f is in Lp(Rd)
and g is in Lq(Rd) and
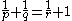
with 1 ≤ p, q ,r ≤ ∞. Then
Here the star denotes convolution
, Lp is Lebesgue space
, and
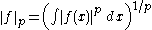
denotes the usual Lp norm.
In case p, q > 1 the result can be strengthened to a sharp form, viz
where the constant cp,q < 1.
An example application is that Young's inequality can be used to show that the heat semigroup
is a contraction semigroup using the L2 norm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of two functions. They are named for William Henry Young
William Henry Young
William Henry Young was an English mathematician. Young was educated at City of London School and Peterhouse, Cambridge. He worked on measure theory, Fourier series, differential calculus amongst other fields, and made brilliant and long-lasting contributions to the study of functions of several...
.
Young's inequality for products can be used to prove Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
. It is also used widely to estimate the norm of nonlinear terms in PDE theory
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, since it allows one to estimate a product of two terms by a sum of the same terms raised to a power and scaled.
Standard version for conjugate Hölder exponents
In its standard form, the inequality states that if a and b are nonnegative real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and p and q are positive real numbers such that 1/p + 1/q = 1, then
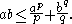
Equality holds if and only if ap = bq. This form of Young's inequality is a special case of the inequality of weighted arithmetic and geometric means and can be used to prove Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
.
Elementary case
An elementary case of Young's inequality is the inequality with exponent 2,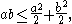
which also gives rise to the so-called Young's inequality with ε (valid for any ε > 0), sometimes called the Peter-Paul inequality:
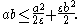
Standard version for increasing functions

let f denote a real-valued, continuous and strictly increasing function on [0, c] with c > 0 and f(0) = 0. Let f−1 denote the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f. Then, for all a ∈ [0, c] and b ∈ [0, f(c)],
with equality if and only if b = f(a).
Generalization using Legendre transforms
If f is a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
and its Legendre transform (convex conjugate
Convex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
) is denoted by g, then
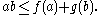
This follows immediately from the definition of the Legendre transform. This inequality also holds — in the form a ·b ≤ f(a) + g(b) — if f is a convex function taking a vector argument .
Examples
- The Legendre transform of f(a) = ap/p is g(b) = bq/q with q such that 1/p + 1/q = 1, and thus Young's inequality for conjugate Hölder exponents mentioned above is a special case.
- The Legendre transform of f(a) = ea – 1 is g(b) = 1 − b + b ln b, hence ab ≤ ea − b + b ln b for all non-negative a and b. This estimate is useful in large deviations theoryLarge deviations theoryIn probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
under exponential moment conditions, because b ln b appears in the definition of relative entropy, which is the rate functionRate functionIn mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
in Sanov's theoremSanov's theoremIn information theory, Sanov's theorem gives a bound on the probability of observing an atypical sequence of samples from a given probability distribution....
.
Young's inequality for convolutions
In real analysisReal analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the following result is also called Young's inequality:
Suppose f is in Lp(Rd)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
and g is in Lq(Rd) and
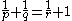
with 1 ≤ p, q ,r ≤ ∞. Then
Here the star denotes convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
, Lp is Lebesgue space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, and
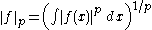
denotes the usual Lp norm.
In case p, q > 1 the result can be strengthened to a sharp form, viz
where the constant cp,q < 1.
An example application is that Young's inequality can be used to show that the heat semigroup
Weierstrass transform
In mathematics, the Weierstrass transform of a function f : R → R, named after Karl Weierstrass, is the function F defined by...
is a contraction semigroup using the L2 norm.
External links
- Young's Inequality at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...