Large deviations theory
Encyclopedia
In probability theory
, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace
and Cramér
, although a clear unified formal definition was introduced in 1966 by Varadhan
. Large deviations theory formalizes the heuristic ideas of concentration of measures and widely generalizes the notion of convergence of probability measures.
Roughly speaking, large deviations theory concerns itself with the exponential decay of the probability measures of certain kinds of extreme or tail events, as the number of observations grows arbitrarily large.
coin. The possible outcomes could be heads or tails. Let us denote the possible outcome of the i-th trial by
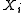, where we encode head as 1 and tail as 0. Now let 
denote the mean value after 
trials, namely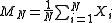
Then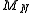
lies between 0 and 1. From the law of large numbers
(and also from our experience) we know that as N grows, the distribution of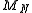
converges to 
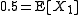almost surely.
Moreover, by the central limit theorem
, we know that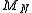
is approximately normally distributed for large 
. The central limit theorem can provide more detailed information about the behavior of 
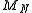than the law of large numbers. For example, we can approximately find a tail probability of 
, 
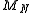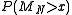, that
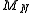is greater than 
, for a fixed value of 
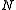. However, the approximation by the CLT may not be accurate if 
is far from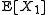 
. Also, it does not provide information about the convergence of the tail probabilities as 
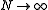. However, the large deviation theory can provide answers for such problems.
Let us make this statement more precise. For a given value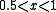
, let us compute the tail probability 
. Define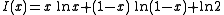
(Note that the function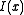
is a convex increasing function.) Then by Chernoff's inequality, it can be shown that 
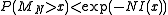. This bound is rather sharp, in the sense that 
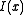cannot be replaced with a larger number which would yield a strict inequality for all positive 
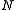. (However, the exponential bound can still be reduced by a subexponential factor on the order of 
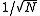.) Hence, we obtain the following result: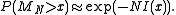
The probability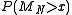
decays exponentially as 
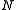grows to infinity, at a rate depending on x. This formula approximates any tail probability of the sample mean of i.i.d. and gives its convergence as the number of samples increases.
independent trial. And for each toss, the probability of getting head or tail is always the
same. This makes the random numbers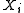
independent and identically distributed (i.i.d.). For i.i.d. variables
whose common distribution satisfies a certain growth condition, large deviation theory states that the following limit exists:
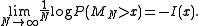
The function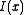
is called the "rate function
" or "Cramér function" or sometimes the "entropy function". Roughly speaking, the existence of this limit is what establishes the above mentioned exponential decay and allows us to conclude that for large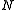
,
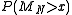takes the form:
which is the basic result of large deviations theory in this setting. Note that the inequality given in the first paragraph, as opposed to the asymptotic formula presented here, need not remain valid in more general settings.
In the i.i.d. setting,
if we know the probability distribution of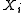
, an explicit
expression for the rate function can be obtained. This is given by a
Legendre–Fenchel transformation,
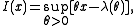
where the function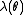
is called the cumulant generating function (CGF), given by
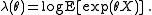
Here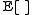
denotes expectation value
with respect to the probability
distribution function of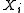
and 
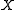is any one of the
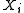s. If 
follows a normal distribution,
the rate function becomes a parabola with its apex at the mean of the normal
distribution.
If the condition of independent identical distribution is relaxed, particularly
if the numbers
are not independent but nevertheless
satisfy the Markov property
, the basic large deviations result stated above can be generalized.
let 
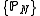be a sequence of Borel
probability measures on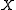
, let 
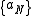be a sequence of positive real numbers such that 
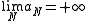, and finally let 
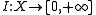be a lower semicontinuous functional on 
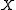. The sequence 
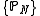is said to satisfy a large deviation principle with speed 
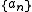and rate 
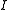if, and only if, for each Borel measurable set 
,
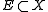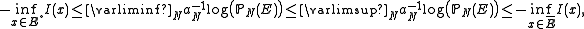
where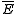
and 
denote respectively the closure
and interior
of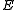
.
Harald Cramér
, who applied them to model the insurance business. From the point
of view of an insurance company, the earning is at a constant rate per month
(the monthly premium) but the claims come randomly. For the company to be successful
over a certain period of time (preferably many months), the total earning should
exceed the total claim. Thus to estimate the premium you have to ask the following
question : "What should we choose as the premium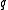
such that over
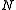months the total claim 
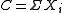should
be less than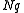
? " This is clearly the same question asked by
the large deviations theory. Cramér gave a solution to this question for i.i.d. random variable
s, where the rate function is expressed as a power series.
The results we have quoted above were later obtained by Chernoff
, among other people. A very
incomplete list of mathematicians who have made important advances would
include S.R.S. Varadhan (who has won the Abel prize), D. Ruelle and O.E. Lanford
.
and risk management
. In Physics, the best known application of large deviations theory arise in Thermodynamics
and Statistical Mechanics
(in connection with relating entropy
with rate function).
in statistical mechanics. This can be heuristically seen
in the following way. In statistical mechanics the entropy of a particular macro-state is related
to the number of micro-states which corresponds to this macro-state. In our coin tossing example the
mean value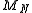
could designate a particular macro-state. And the particular sequence of
heads and tails which gives rise to a particular value of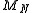
constitutes a particular
micro-state. Loosely speaking a macro-state having a higher number of micro-states giving rise to it,
has higher entropy. And a state with higher entropy has a higher chance of being realised in actual
experiments. The macro-state with mean value of zero (as many heads as tails) has the highest number micro-states giving rise to it and it is indeed the state with the highest entropy. And in most practical situation
we shall indeed obtain this macro-state for large number of trials. The "rate function" on the other
hand measures the probability of appearance of a particular macro-state. The smaller the rate function
the higher is the chance of a macro-state appearing. In our coin-tossing the value of the "rate function" for mean value equal to zero is zero. In this way one can see the "rate function" as the negative of the "entropy".
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
and Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
, although a clear unified formal definition was introduced in 1966 by Varadhan
S. R. Srinivasa Varadhan
Sathamangalam Ranga Iyengar Srinivasa Varadhan FRS is an Indian-American mathematician from Madras , Tamil Nadu, India.-Biography:...
. Large deviations theory formalizes the heuristic ideas of concentration of measures and widely generalizes the notion of convergence of probability measures.
Roughly speaking, large deviations theory concerns itself with the exponential decay of the probability measures of certain kinds of extreme or tail events, as the number of observations grows arbitrarily large.
An elementary example
Consider a sequence of independent tosses of a faircoin. The possible outcomes could be heads or tails. Let us denote the possible outcome of the i-th trial by
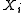, where we encode head as 1 and tail as 0. Now let denote the mean value after trials, namely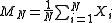Then
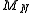lies between 0 and 1. From the law of large numbersLaw of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
(and also from our experience) we know that as N grows, the distribution of
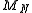converges to 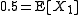almost surely.Moreover, by the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, we know that
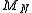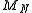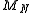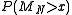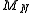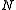is approximately normally distributed for large . The central limit theorem can provide more detailed information about the behavior of than the law of large numbers. For example, we can approximately find a tail probability of , , that is greater than , for a fixed value of . However, the approximation by the CLT may not be accurate if is far from 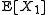. Also, it does not provide information about the convergence of the tail probabilities as 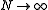. However, the large deviation theory can provide answers for such problems.Let us make this statement more precise. For a given value
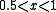, let us compute the tail probability . Define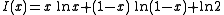(Note that the function
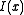is a convex increasing function.) Then by Chernoff's inequality, it can be shown that 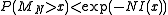. This bound is rather sharp, in the sense that 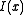cannot be replaced with a larger number which would yield a strict inequality for all positive 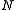. (However, the exponential bound can still be reduced by a subexponential factor on the order of 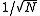.) Hence, we obtain the following result: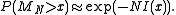The probability
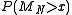decays exponentially as 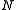grows to infinity, at a rate depending on x. This formula approximates any tail probability of the sample mean of i.i.d. and gives its convergence as the number of samples increases.Large deviations for sums of independent random variables
In the above example of coin-tossing, we explicitly assumed that each toss is anindependent trial. And for each toss, the probability of getting head or tail is always the
same. This makes the random numbers
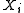independent and identically distributed (i.i.d.). For i.i.d. variableswhose common distribution satisfies a certain growth condition, large deviation theory states that the following limit exists:
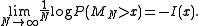
The function
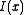is called the "rate functionRate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
" or "Cramér function" or sometimes the "entropy function". Roughly speaking, the existence of this limit is what establishes the above mentioned exponential decay and allows us to conclude that for large
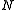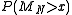, takes the form:which is the basic result of large deviations theory in this setting. Note that the inequality given in the first paragraph, as opposed to the asymptotic formula presented here, need not remain valid in more general settings.
In the i.i.d. setting,
if we know the probability distribution of
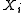, an explicitexpression for the rate function can be obtained. This is given by a
Legendre–Fenchel transformation,
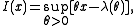
where the function
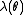is called the cumulant generating function (CGF), given by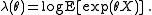Here
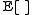denotes expectation valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to the probability
distribution function of
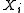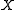and is any one of the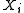s. If follows a normal distribution,the rate function becomes a parabola with its apex at the mean of the normal
distribution.
If the condition of independent identical distribution is relaxed, particularly
if the numbers
are not independent but neverthelesssatisfy the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
, the basic large deviations result stated above can be generalized.
Formal definition
Given a Polish spacePolish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
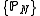let be a sequence of BorelBorel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
probability measures on
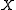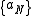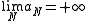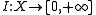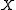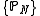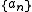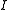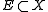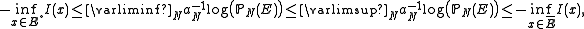
, let be a sequence of positive real numbers such that , and finally let be a lower semicontinuous functional on . The sequence is said to satisfy a large deviation principle with speed and rate if, and only if, for each Borel measurable set ,where
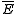and denote respectively the closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
and interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of
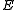.Brief history
The first rigorous results concerning large deviations are due to the Swedish mathematicianHarald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
, who applied them to model the insurance business. From the point
of view of an insurance company, the earning is at a constant rate per month
(the monthly premium) but the claims come randomly. For the company to be successful
over a certain period of time (preferably many months), the total earning should
exceed the total claim. Thus to estimate the premium you have to ask the following
question : "What should we choose as the premium
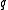such that over 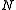months the total claim 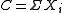shouldbe less than
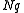? " This is clearly the same question asked bythe large deviations theory. Cramér gave a solution to this question for i.i.d. random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, where the rate function is expressed as a power series.
The results we have quoted above were later obtained by Chernoff
Herman Chernoff
Herman Chernoff is an American applied mathematician, statistician and physicist formerly a professor at MIT and currently working at Harvard University.-Education:* Ph.D., Applied Mathematics, 1948. Brown University....
, among other people. A very
incomplete list of mathematicians who have made important advances would
include S.R.S. Varadhan (who has won the Abel prize), D. Ruelle and O.E. Lanford
Oscar Lanford
Oscar Eramus Lanford III is an American mathematician working on mathematical physics and dynamical systems theory. He was awarded his undergraduate degree from Wesleyan University and the Ph.D. from Princeton University in 1966 under the supervision of Arthur Wightman...
.
Applications
Principles of large deviations may be effectively applied to gather information out of a probabilistic model. Thus, theory of large deviations finds its applications in information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and risk management
Risk management
Risk management is the identification, assessment, and prioritization of risks followed by coordinated and economical application of resources to minimize, monitor, and control the probability and/or impact of unfortunate events or to maximize the realization of opportunities...
. In Physics, the best known application of large deviations theory arise in Thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
and Statistical Mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
(in connection with relating entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
with rate function).
Large deviations and entropy
The rate function is related to the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
in statistical mechanics. This can be heuristically seen
in the following way. In statistical mechanics the entropy of a particular macro-state is related
to the number of micro-states which corresponds to this macro-state. In our coin tossing example the
mean value
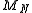could designate a particular macro-state. And the particular sequence ofheads and tails which gives rise to a particular value of
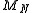constitutes a particularmicro-state. Loosely speaking a macro-state having a higher number of micro-states giving rise to it,
has higher entropy. And a state with higher entropy has a higher chance of being realised in actual
experiments. The macro-state with mean value of zero (as many heads as tails) has the highest number micro-states giving rise to it and it is indeed the state with the highest entropy. And in most practical situation
we shall indeed obtain this macro-state for large number of trials. The "rate function" on the other
hand measures the probability of appearance of a particular macro-state. The smaller the rate function
the higher is the chance of a macro-state appearing. In our coin-tossing the value of the "rate function" for mean value equal to zero is zero. In this way one can see the "rate function" as the negative of the "entropy".
See also
- Chernoff's inequality
- Contraction principle (large deviations theory)Contraction principle (large deviations theory)In mathematics — specifically, in large deviations theory — the contraction principle is a theorem that states how a large deviation principle on one space "pushes forward" to a large deviation principle on another space via a continuous function.-Statement of the theorem:Let X and Y be...
, a result on how large deviations principles "push forwardPush forwardSuppose that φ : M → N is a smooth map between smooth manifolds; then the differential of φ at a point x is, in some sense, the best linear approximation of φ near x. It can be viewed as a generalization of the total derivative of ordinary calculus...
" - Freidlin–Wentzell theorem, a large deviations principle for Itō diffusionIto diffusionIn mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
s - Laplace principleLaplace principle (large deviations theory)In mathematics, Laplace's principle is a basic theorem in large deviations theory, similar to Varadhan's lemma. It gives an asymptotic expression for the Lebesgue integral of exp over a fixed set A as θ becomes large...
, a large deviations principle in Rd - Schilder's theoremSchilder's theoremIn mathematics, Schilder's theorem is a result in the large deviations theory of stochastic processes. Roughly speaking, Schilder's theorem gives an estimate for the probability that a sample path of Brownian motion will stray far from the mean path . This statement is made precise using rate...
, a large deviations principle for Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications... - Varadhan's lemmaVaradhan's lemmaIn mathematics, Varadhan's lemma is a result in large deviations theory named after S. R. Srinivasa Varadhan. The result gives information on the asymptotic distribution of a statistic φ of a family of random variables Zε as ε becomes small in terms of a rate function for the variables.-Statement...
- Extreme value theoryExtreme value theoryExtreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
- Large deviations of Gaussian random functionsLarge deviations of Gaussian random functionsA random function – of either one variable , or two or more variables – is called Gaussian if every finite-dimensional distribution is a multivariate normal distribution. Gaussian random fields on the sphere are useful when analysing* the anomalies in the cosmic microwave background...