
Contraction principle (large deviations theory)
Encyclopedia
In mathematics
— specifically, in large deviations theory
— the contraction principle is a theorem
that states how a large deviation principle on one space "pushes forward
" to a large deviation principle on another space via a continuous function
.
topological space
s and let (με)ε>0 be a family of probability measure
s on X that satisfies the large deviation principle with rate function
I : X → [0, +∞]. Let T : X → Y be a continuous function, and let νε = T∗(με) be the push-forward measure
of με by T, i.e., for each measurable set/event E ⊆ Y, νε(E) = με(T−1(E)). Let
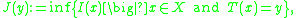
with the convention that the infimum
of I over the empty set
∅ is +∞. Then:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
— the contraction principle is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
that states how a large deviation principle on one space "pushes forward
Push forward
Suppose that φ : M → N is a smooth map between smooth manifolds; then the differential of φ at a point x is, in some sense, the best linear approximation of φ near x. It can be viewed as a generalization of the total derivative of ordinary calculus...
" to a large deviation principle on another space via a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
Statement of the theorem
Let X and Y be HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and let (με)ε>0 be a family of probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on X that satisfies the large deviation principle with rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
I : X → [0, +∞]. Let T : X → Y be a continuous function, and let νε = T∗(με) be the push-forward measure
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
of με by T, i.e., for each measurable set/event E ⊆ Y, νε(E) = με(T−1(E)). Let
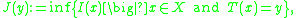
with the convention that the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of I over the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ is +∞. Then:
- J : Y → [0, +∞] is a rate function on Y,
- J is a good rate function on Y if I is a good rate function on X, and
- (νε)ε>0 satisfies the large deviation principle on Y with rate function J.

