
Young symmetrizer
Encyclopedia
In mathematics
, a Young symmetrizer is an element of the group algebra
of the symmetric group
, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex number
s. A similar construction works over any field, and the resulting representations are called Specht module
s. The Young symmetrizer is named after British mathematician Alfred Young
.
λ corresponding to a numbered partition of n, define two permutation subgroups
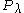 and
and 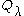 of Sn as follows:
of Sn as follows:
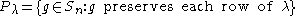
and
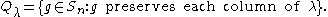
Corresponding to these two subgroups, define two vectors in the group algebra
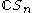 as
as
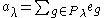
and
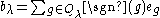
where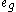 is the unit vector corresponding to g, and
is the unit vector corresponding to g, and 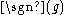 is the signature of the permutation. The product
is the signature of the permutation. The product
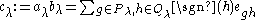
is the Young symmetrizer corresponding to the Young tableau
λ. Each Young symmetrizer corresponds to an irreducible representation of the symmetric group, and every irreducible representation can be obtained from a corresponding Young symmetrizer. (If we replace the complex number
s by more general field
s the corresponding representations will not be irreducible in general.)
over the complex number
s. Consider then the tensor product
vector space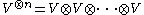 (n times). Let Sn act on this tensor product space by permuting each index. One then has a natural group algebra
(n times). Let Sn act on this tensor product space by permuting each index. One then has a natural group algebra
representation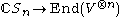 on endomorphism
on endomorphism
s on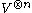 .
.
Given a partition λ of n, so that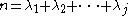 , then the image
, then the image
of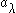 is
is
The image of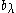 is
is
where μ is the conjugate partition to λ. Here, and
and 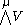 are the symmetric
are the symmetric
and alternating tensor product spaces
.
The image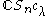 of
of 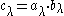 in
in  is an irreducible representation of Sn, called a Specht module
is an irreducible representation of Sn, called a Specht module
. We write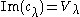
for the irreducible representation.
Some scalar multiple of is idempotent, that is
is idempotent, that is 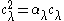 for some rational number
for some rational number  . Specifically, one finds
. Specifically, one finds 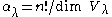 . In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra
. In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra 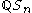 .
.
Consider, for example, S3 and the partition (2,1). Then one has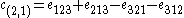
If V is a complex vector space, then
the images of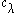 on spaces Vd provides essentially all the finite-dimensional irreducible representations of GL(V).
on spaces Vd provides essentially all the finite-dimensional irreducible representations of GL(V).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Young symmetrizer is an element of the group algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. A similar construction works over any field, and the resulting representations are called Specht module
Specht module
In mathematics, a Specht module is one of the representations of symmetric groups studied by .They are indexed by partitions, and in characteristic 0 the Specht modules of partitions of n form a complete set of irreducible representations of the symmetric group on n points.-Definition:Fix a...
s. The Young symmetrizer is named after British mathematician Alfred Young
Alfred Young
Alfred Young, FRS was a British mathematician.He was born in Widnes, Lancashire, England and educated at Monkton Combe School in Somerset and Clare College, Cambridge, graduating BA as 10th Wrangler in 1895. He is known for his work in the area of group theory...
.
Definition
Given a finite symmetric group Sn and specific Young tableauYoung tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
λ corresponding to a numbered partition of n, define two permutation subgroups
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
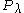 and
and 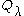 of Sn as follows:
of Sn as follows: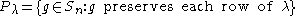
and
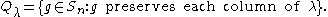
Corresponding to these two subgroups, define two vectors in the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
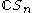 as
as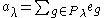
and
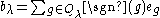
where
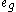 is the unit vector corresponding to g, and
is the unit vector corresponding to g, and 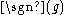 is the signature of the permutation. The product
is the signature of the permutation. The product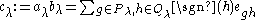
is the Young symmetrizer corresponding to the Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
λ. Each Young symmetrizer corresponds to an irreducible representation of the symmetric group, and every irreducible representation can be obtained from a corresponding Young symmetrizer. (If we replace the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s by more general field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s the corresponding representations will not be irreducible in general.)
Construction
Let V be any vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Consider then the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
vector space
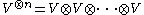 (n times). Let Sn act on this tensor product space by permuting each index. One then has a natural group algebra
(n times). Let Sn act on this tensor product space by permuting each index. One then has a natural group algebraGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
representation
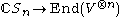 on endomorphism
on endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s on
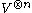 .
.Given a partition λ of n, so that
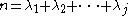 , then the image
, then the imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of
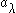 is
is
The image of
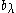 is
is
where μ is the conjugate partition to λ. Here,
 and
and 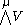 are the symmetric
are the symmetricSymmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
and alternating tensor product spaces
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
.
The image
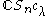 of
of 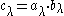 in
in  is an irreducible representation of Sn, called a Specht module
is an irreducible representation of Sn, called a Specht moduleSpecht module
In mathematics, a Specht module is one of the representations of symmetric groups studied by .They are indexed by partitions, and in characteristic 0 the Specht modules of partitions of n form a complete set of irreducible representations of the symmetric group on n points.-Definition:Fix a...
. We write
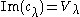
for the irreducible representation.
Some scalar multiple of
 is idempotent, that is
is idempotent, that is 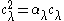 for some rational number
for some rational number  . Specifically, one finds
. Specifically, one finds 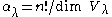 . In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra
. In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra 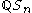 .
.Consider, for example, S3 and the partition (2,1). Then one has
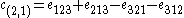
If V is a complex vector space, then
the images of
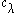 on spaces Vd provides essentially all the finite-dimensional irreducible representations of GL(V).
on spaces Vd provides essentially all the finite-dimensional irreducible representations of GL(V).

